６章　学習に関するテクニック　正則化, Weight decay, Dropout 『ゼロから作るDeep Learning』

f:id:kaeken:20161112190945p:plain 続いて、正則化について。

過学習overfittingの起きる主な２つの原因

・パラメータを大量に持ち、表現力の高いモデルであること
・訓練データが少ないこと

敢えて過学習させたケースをサンプルコードで確認する

# cat overfit_weight_decay_pre_save.py

# coding: utf-8
import os
import sys

sys.path.append(os.pardir)  # 親ディレクトリのファイルをインポートするための設定
import numpy as np
import matplotlib.pyplot as plt
plt.switch_backend('agg')

from dataset.mnist import load_mnist
from common.multi_layer_net import MultiLayerNet
from common.optimizer import SGD

(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)

# 過学習を再現するために、学習データを削減
x_train = x_train[:300]
t_train = t_train[:300]

weight_decay_lambda = 0
#weight_decay_lambda = 0.1
network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10,
                        weight_decay_lambda=weight_decay_lambda)
optimizer = SGD(lr=0.01)

max_epochs = 201
train_size = x_train.shape[0]
batch_size = 100

train_loss_list = []
train_acc_list = []
test_acc_list = []

iter_per_epoch = max(train_size / batch_size, 1)
epoch_cnt = 0

for i in range(1000000000):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]

    grads = network.gradient(x_batch, t_batch)
    optimizer.update(network.params, grads)

    if i % iter_per_epoch == 0:
        train_acc = network.accuracy(x_train, t_train)
        test_acc = network.accuracy(x_test, t_test)
        train_acc_list.append(train_acc)
        test_acc_list.append(test_acc)

        print("epoch:" + str(epoch_cnt) + ", train acc:" + str(train_acc) + ", test acc:" + str(test_acc))

        epoch_cnt += 1
        if epoch_cnt >= max_epochs:
            break



# 3.グラフの描画==========
markers = {'train': 'o', 'test': 's'}
x = np.arange(max_epochs)
plt.plot(x, train_acc_list, marker='o', label='train', markevery=10)
plt.plot(x, test_acc_list, marker='s', label='test', markevery=10)
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
#plt.show()
plt.savefig('overfit_weight_decay_pre.png')

訓練データの認識精度が100%になり、テストデータと大きく乖離していることが分かる。 f:id:kaeken:20161112190917p:plain

そこで過学習抑制のため荷重減衰weight decayという手法を使う。以下のように正則化の強さをコントールするハイパーパラメータを0.1に変更する

# diff overfit_weight_decay_pre_save.py overfit_weight_decay_save.py
20,21c20,21
< weight_decay_lambda = 0
< #weight_decay_lambda = 0.1
---
> #weight_decay_lambda = 0
> weight_decay_lambda = 0.1
68c68
< plt.savefig('overfit_weight_decay_pre.png')
---
> plt.savefig('overfit_weight_decay.png')

訓練データの認識精度が100%ではなくなり、テストデータとの乖離が小さくなっていることが分かる。 f:id:kaeken:20161112190945p:plain

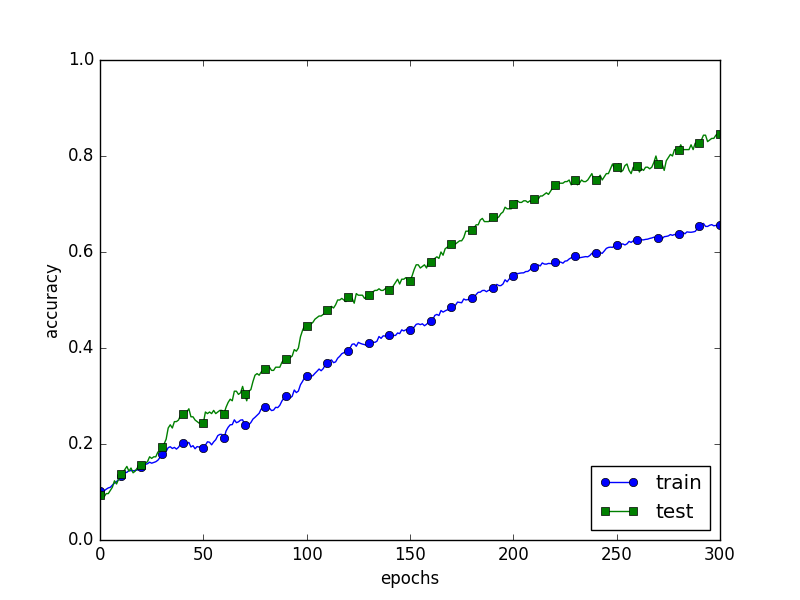
続いて、Dropoutという過学習抑制手法について。

Dropoutとは：ニューロンをランダムに消去しながら学習する手法

以下実行したサンプルコード

# cat overfit_dropout_save.py

# coding: utf-8
import os
import sys
sys.path.append(os.pardir)  # 親ディレクトリのファイルをインポートするための設定
import numpy as np
import matplotlib.pyplot as plt
plt.switch_backend('agg')

from dataset.mnist import load_mnist
from common.multi_layer_net_extend import MultiLayerNetExtend
from common.trainer import Trainer

(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)

# 過学習を再現するために、学習データを削減
x_train = x_train[:300]
t_train = t_train[:300]

use_dropout = True  # Dropoutなしのときの場合はFalseに
dropout_ratio = 0.15
network = MultiLayerNetExtend(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100],
                              output_size=10, use_dropout=use_dropout, dropout_ration=dropout_ratio)
trainer = Trainer(network, x_train, t_train, x_test, t_test,
                  epochs=301, mini_batch_size=100,
                  optimizer='sgd', optimizer_param={'lr': 0.01}, verbose=True)
trainer.train()

train_acc_list, test_acc_list = trainer.test_acc_list, trainer.train_acc_list

# グラフの描画==========
markers = {'train': 'o', 'test': 's'}
x = np.arange(len(train_acc_list))
plt.plot(x, train_acc_list, marker='o', label='train', markevery=10)
plt.plot(x, test_acc_list, marker='s', label='test', markevery=10)
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
#plt.show()
plt.savefig('overfit_dropout.png')