深層学習用の数学プログラミングは『Pythonからはじめる数学入門』より『行列プログラマー』かも

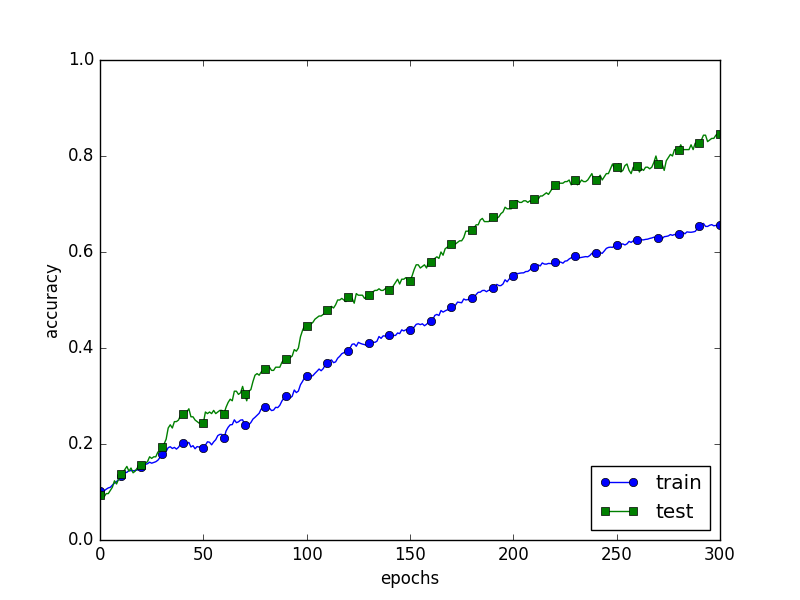
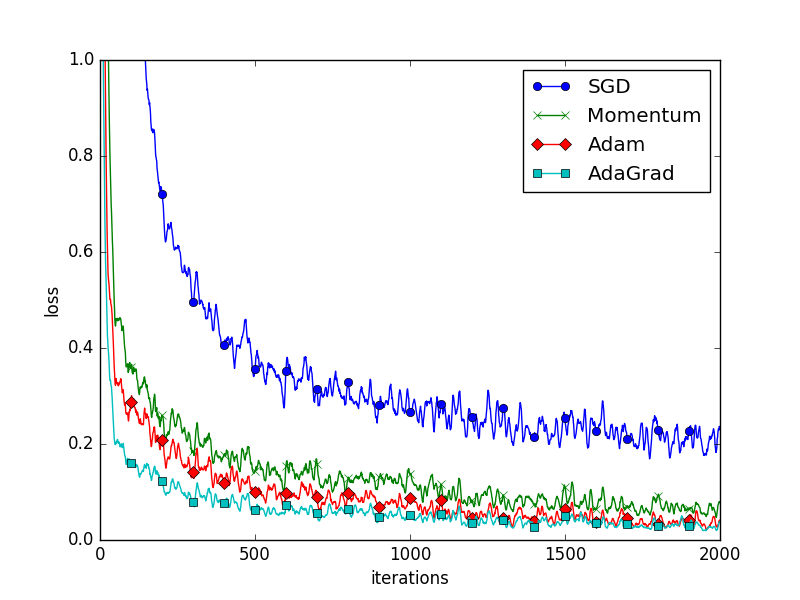
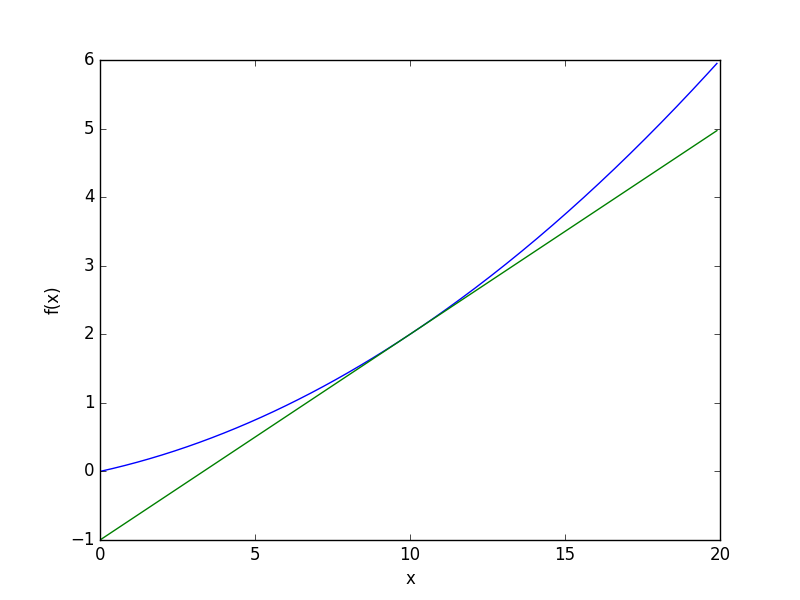
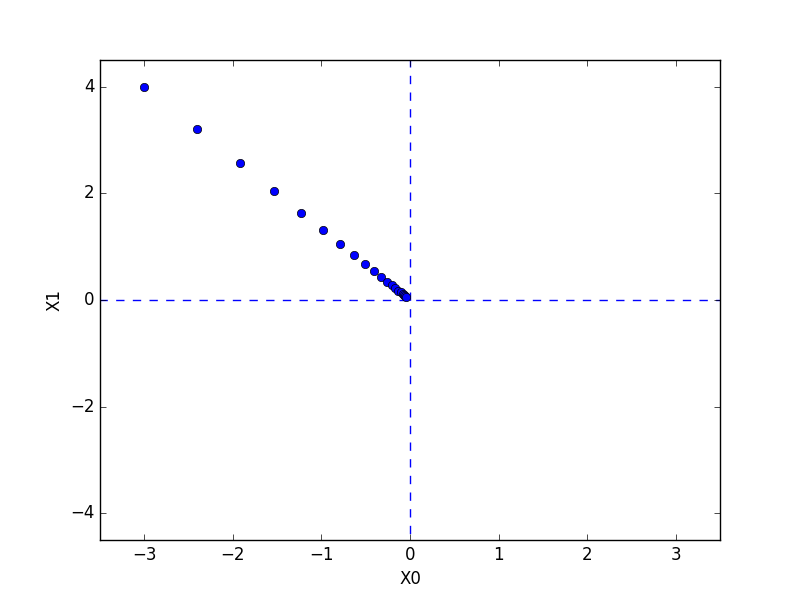
以下、手を動かしていないが、いったん通読完了。

www.oreilly.co.jp

目次

1章　数を扱う
    1.1　基本数学演算
    1.2　ラベル：名前に数を割り当てる
    1.3　さまざまな種類の数
        1.3.1　分数を扱う
        1.3.2　複素数
    1.4　ユーザ入力を受け取る
        1.4.1　例外と不当入力の処理
        1.4.2　分数と複素数を入力
    1.5　数学を行うプログラムを書く
        1.5.1　整数の因数を計算する
        1.5.2　乗算表を生成する
        1.5.3　測定単位を変換する
        1.5.4　2次方程式の解を求める
    1.6　学んだこと
    1.7　プログラミングチャレンジ
        問題1-1　奇数偶数自動判別プログラム
        問題1-2　乗算表生成器の拡張
        問題1-3　単位変換プログラムの拡張
        問題1-4　分数電卓
        問題1-5　ユーザに脱出能力を与える

2章　データをグラフで可視化する
    2.1　デカルト座標平面を理解する
    2.2　リストとタプルの操作
        2.2.1　リストやタプルで繰り返す
    2.3　matplotlibでグラフを作る
        2.3.1　グラフで点を作る
        2.3.2　ニューヨーク市の年間平均気温をグラフ化する
        2.3.3　ニューヨーク市の月間気温傾向を比較する
        2.3.4　グラフのカスタマイズ
        2.3.5　プロットの保存
    2.4　式をプロットする
        2.4.1　ニュートンの万有引力の法則
        2.4.2　投射運動
    2.5　学んだこと
    2.6　プログラミングチャレンジ
        問題2-1　1日の間に気温はどのように変化するか
        問題2-2　2次関数を視覚的に探索する
        問題2-3　投射軌跡比較プログラムの拡張
        問題2-4　支出を可視化する
        問題2-5　フィボナッチ数列と黄金比の関係を調べる

3章　データを統計量で記述する
    3.1　平均を求める
    3.2　中央値を求める
    3.3　最頻値を求め度数分布表を作る
        3.3.1　一番多い要素を見つける
        3.3.2　最頻値を探す
        3.3.3　度数分布表を作る
    3.4　散らばりを測る
        3.4.1　数集合の範囲を決める
        3.4.2　分散と標準偏差を求める
    3.5　2つのデータセットの相関を計算する
        3.5.1　相関係数を計算する
        3.5.2　高校の成績と大学入試の点数
    3.6　散布図
    3.7　ファイルからデータを読み込む
        3.7.1　テキストファイルからデータを読み込む
        3.7.2　CSVファイルからデータを読み込む
    3.8　学んだこと
    3.9　プログラミングチャレンジ
        問題3-1　よりよい相関係数を求めるプログラム
        問題3-2　統計電卓
        問題3-3　他のCSVデータでの実験
        問題3-4　百分位を求める
        問題3-5　グループ度数分布表を作る

4章　SymPyで代数と式を計算する
    4.1　式の記号と記号演算を定義する
    4.2　式を扱う
        4.2.1　式の因数分解と展開
        4.2.2　プリティプリント
        4.2.3　値に代入する
        4.2.4　文字列を数式に変換する
    4.3　方程式を解く
        4.3.1　2次方程式を解く
        4.3.2　1変数を他の変数について解く
        4.3.3　連立方程式を解く
    4.4　SymPyを使ってプロットする
        4.4.1　ユーザが入力した式をプロットする
        4.4.2　複数の関数をプロットする
    4.5　学んだこと
    4.6　プログラミングチャレンジ
        問題4-1　因数ファインダ
        問題4-2　グラフを使った方程式ソルバー
        問題4-3　級数の和
        問題4-4　1変数の不等式を解く
        ヒント：役立つ関数

5章　集合と確率を操作する
    5.1　集合とは何か
        5.1.1　集合の構成
        5.1.2　部分集合、上位集合、べき集合
        5.1.3　集合演算
    5.2　確率
        5.2.1　事象Aまたは事象Bの確率
        5.2.2　事象Aおよび事象Bの確率
        5.2.3　乱数生成
        5.2.4　非一様乱数
    5.3　学んだこと
    5.4　プログラミングチャレンジ
        問題5-1　ベン図を使って集合の関係を可視化する
        問題5-2　大数の法則
        問題5-3　お金がなくなるまで何回硬貨を投げられるか
        問題5-4　トランプをよく切る
        問題5-5　円の領域を推定する
        πの値を推定する

6章　幾何図形とフラクタルを描画する
    6.1　matplotlibのパッチで幾何図形を描く
        6.1.1　円を描く
        6.1.2　図形のアニメーションを作る
        6.1.3　投射軌跡のアニメーション
    6.2　フラクタルを描く
        6.2.1　平面上の点の変換
        6.2.2　バーンスレイのシダを描く
    6.3　学んだこと
    6.4　プログラミングチャレンジ
        問題6-1　正方形に円を詰める
        問題6-2　シェルピンスキーの三角形
        問題6-3　エノンの関数を調べる
        問題6-4　マンデルブロ集合を描く
        imshow()関数
        リストのリストを作る
        マンデルブロ集合を描く

7章　初等解析問題を解く
    7.1　関数とは何か
        7.1.1　関数の定義域と値域
        7.1.2　よく使われる数学関数
    7.2　SymPyでの仮定
    7.3　関数の極限を求める
        7.3.1　連続複利（Continuous Compound Interest）
        7.3.2　瞬間変化率
    7.4　関数の微分を求める
        7.4.1　微分電卓
        7.4.2　偏微分を求める
    7.5　高階微分と極大極小の計算
    7.6　勾配上昇法を用いて最大値を求める
        7.6.1　勾配上昇法のジェネリックなプログラム
        7.6.2　初期値について一言
        7.6.3　ステップサイズとイプシロンの役割
    7.7　関数の積分を求める
    7.8　確率密度関数
    7.9　学んだこと
    7.10　プログラミングチャレンジ
        問題7-1　ある点での関数の連続性を検証する
        問題7-2　勾配降下法を実装する
        問題7-3　2曲線で囲まれた領域の面積
        問題7-4　曲線の長さを求める

付録A　ソフトウェアのインストール
    A.1　Microsoft Windows
        A.1.1　SymPyの更新
        A.1.2　matplotlib-vennのインストール
        A.1.3　Pythonシェルの開始
    A.2　Linux
        A.2.1　SymPyの更新
        A.2.2　matplotlib-vennのインストール
        A.2.3　Pythonシェルの開始
    A.3　Mac OS X
        A.3.1　SymPyの更新
        A.3.2　matplotlib-vennのインストール
        A.3.3　Pythonシェルの開始

付録B　Pythonについて
    B.1　if __name__ == '__main__' 
    B.2　リスト内包表記
    B.3　辞書データ構造
    B.4　複数戻り値
    B.5　例外処理
        B.5.1　複数の例外型を指定する
        B.5.2　elseブロック
    B.6　Pythonでのファイル読み込み
        B.6.1　全行を一度に読み込む
        B.6.2　ファイル名を入力で指定する
        B.6.3　ファイル読み込み時のエラー処理
    B.7　コードの再利用

Pythonを使っていろいろな数学のプログラミングを仕方のポイントを学べる点で有益だった。

ただ、正直、深層学習をやる分には関係のない分野もあり、それよりも、

『ゼロから作るDeep Learning』を学ぶ過程で必要だと感じたことは、

行列プログラミングの徹底的な理解。

その意味では、以下の分厚い行列に特化した参考書のほうがよいかもしれない（こっちは未読）。

www.oreilly.co.jp

0章　関数（とその他の数学とコンピュータに関する予備知識）
    0.1　集合に関する用語と記法
    0.2　デカルト積
    0.3　関数
        0.3.1　関数 vs プロシージャ vs 計算問題
        0.3.2　関数に関連する2つの計算問題
        0.3.3　特定の定義域と余定義域を持つ関数の集合に関する記法
        0.3.4　恒等関数
        0.3.5　関数の合成
        0.3.6　関数の合成の結合則
        0.3.7　逆関数
        0.3.8　可逆関数の合成関数についての可逆性
    0.4　確率
        0.4.1　確率分布
        0.4.2　事象及び確率の和
        0.4.3　関数への無作為な入力
        0.4.4　完全秘匿
        0.4.5　完全秘匿で可逆な関数
    0.5　ラボ：Python入門..集合、リスト、辞書、内包表記
        0.5.1　簡単な式
        0.5.2　代入文
        0.5.3　条件式
        0.5.4　集合
        0.5.5　リスト
        0.5.6　タプル
        0.5.7　その他の繰り返し処理について
        0.5.8　辞書
        0.5.9　1行プロシージャを定義する
    0.6　ラボ：Pythonと逆インデックス..モジュールと制御構造
        0.6.1　既存のモジュールの利用
        0.6.2　モジュールの作成
        0.6.3　ループと条件文
        0.6.4　字下げによるPythonのグループ化機能
        0.6.5　ループからの脱出
        0.6.6　ファイルからの読み込み
        0.6.7　ミニ検索エンジン
    0.7　確認用の質問
    0.8　問題

1章　体
    1.1　複素数入門
    1.2　Pythonにおける複素数
    1.3　体への抽象化
    1.4　Cと遊ぼう
        1.4.1　複素数の絶対値
        1.4.2　複素数を足すこと
        1.4.3　複素数に正の実数を掛けること
        1.4.4　複素数に負の実数を掛けること：180度の回転
        1.4.5　iを掛けること：90度の回転
        1.4.6　複素平面上の単位円：偏角と角度
        1.4.7　オイラーの公式
        1.4.8　複素数の極表示
        1.4.9　指数の第1法則
        1.4.10　ラジアンの回転
        1.4.11　変換の合成
        1.4.12　2次元を越えて
    1.5　GF(2)で遊ぼう
        1.5.1　完全秘匿な暗号化システム、再訪
        1.5.2　ワンタイムパッド
        1.5.3　ネットワークコーディング
    1.6　確認用の質問
    1.7　問題

2章　ベクトル
    2.1　ベクトルとは何か？
    2.2　ベクトルは関数
        2.2.1　Pythonの辞書を用いたベクトルの表現
        2.2.2　スパース性
    2.3　ベクトルで何が表現できるか？
    2.4　ベクトルの加法
        2.4.1　平行移動とベクトルの加法
        2.4.2　ベクトルの加法の結合則と可換則
        2.4.3　矢印としてのベクトル
    2.5　スカラーとベクトルの積
        2.5.1　矢印のスケーリング
        2.5.2　スカラーとベクトルの積の結合則
        2.5.3　原点を通る線分
        2.5.4　原点を通る直線
    2.6　ベクトルの和とスカラーとの積の組み合わせ
        2.6.1　原点を通らない線分と直線
        2.6.2　スカラーとベクトルの積とベクトルの和に対する分配則
        2.6.3　はじめての凸結合
        2.6.4　はじめてのアフィン結合
    2.7　辞書によるベクトルの表現
        2.7.1　セッターとゲッター
        2.7.2　スカラーとベクトルの積
        2.7.3　加法
        2.7.4　ベクトルの反転、ベクトルの和、差の可逆性
    2.8　GF(2)上のベクトル
        2.8.1　完全秘匿性、再再訪
        2.8.2　GF(2)を用いた1か0の秘密共有
        2.8.3　ライツアウト
    2.9　ドット積
        2.9.1　総費用と利益
        2.9.2　線形方程式
        2.9.3　類似性の測定
        2.9.4　GF(2)上のベクトルのドット積
        2.9.5　パリティビット
        2.9.6　簡単な認証方式
        2.9.7　この簡単な認証方式への攻撃
        2.9.8　ドット積の代数的性質
        2.9.9　簡単な認証方式への攻撃、再訪
    2.10　Vecの実装
        2.10.1　Vecを扱う構文
        2.10.2　実装
        2.10.3　Vecの利用
        2.10.4　Vecの表示
        2.10.5　Vecのコピー
        2.10.6　リストからVecへ
    2.11　上三角線形方程式系を解く
        2.11.1　上三角線形方程式系
        2.11.2　後退代入
        2.11.3　後退代入の最初の実装
        2.11.4　このアルゴリズムはどのような場合に役に立つか？
        2.11.5　任意の定義域のベクトルを用いた後退代入
    2.12　ラボ：ドット積を用いた投票記録の比較
        2.12.1　動機
        2.12.2　ファイルから読み込む
        2.12.3　ドット積を用いてベクトルを比較する2つの方法
        2.12.4　ポリシーの比較
        2.12.5　平均的でない民主党員
        2.12.6　宿敵
        2.12.7　更なる課題
    2.13　確認用の質問
    2.14　問題

3章　ベクトル空間
    3.1　線形結合
        3.1.1　線形結合の定義
        3.1.2　線形結合の利用
        3.1.3　係数から線形結合へ
        3.1.4　線形結合から係数へ
    3.2　線形包
        3.2.1　線形包の定義
        3.2.2　他の方程式を含む線形方程式系
        3.2.3　生成子
        3.2.4　線形結合の線形結合
        3.2.5　標準生成子
    3.3　ベクトルの集合の幾何学
        3.3.1　R上のベクトルの線形包の幾何学
        3.3.2　同次線形系の解集合の幾何学
        3.3.3　原点を含むフラットの2通りの表現
    3.4　ベクトル空間
        3.4.1　2つの表現に共通するものは何か？
        3.4.2　ベクトル空間の定義と例
        3.4.3　部分空間
        3.4.4　*抽象ベクトル空間
    3.5　アフィン空間
        3.5.1　原点を通らないフラット
        3.5.2　アフィン結合
        3.5.3　アフィン空間
        3.5.4　線形系の解集合によるアフィン空間の表現
        3.5.5　2通りの表現について、再訪
    3.6　同次線形系とその他の線形系
        3.6.1　同次線形系と対応する一般の線形系
        3.6.2　解の個数、再訪
        3.6.3　平面と直線の交差について
        3.6.4　チェックサム関数
    3.7　確認用の質問
    3.8　問題

4章　行列
    4.1　行列とは何か？
        4.1.1　伝統的な行列
        4.1.2　行列の正体
        4.1.3　行、列、要素
        4.1.4　Pythonにおける行列の実装
        4.1.5　単位行列
        4.1.6　行列の表現間の変換
        4.1.7　matutil.py
    4.2　列ベクトル空間と行ベクトル空間
    4.3　ベクトルとしての行列
    4.4　転置
    4.5　線形結合による行列とベクトルの積及びベクトルと行列の積の表現
        4.5.1　線形結合による行列とベクトルの積の表現
        4.5.2　線形結合によるベクトルと行列の積の表現
        4.5.3　ベクトルの線形結合による表現の行列とベクトルの方程式による定式化
        4.5.4　行列とベクトルの方程式を解く
    4.6　ドット積による行列とベクトルの積の表現
        4.6.1　定義
        4.6.2　応用例
        4.6.3　線形方程式の行列とベクトルの方程式としての定式化
        4.6.4　三角系と三角行列
        4.6.5　行列とベクトルの積の代数的性質
    4.7　ヌル空間
        4.7.1　同次線形系と行列の方程式
        4.7.2　行列とベクトルの方程式の解空間
        4.7.3　はじめてのエラー訂正コード
        4.7.4　線形符号
        4.7.5　ハミングコード
    4.8　スパース行列とベクトルの積の計算
    4.9行列と関数
        4.9.1　行列から関数へ
        4.9.2　関数から行列へ
        4.9.3　行列の導出例
    4.10　線形関数
        4.10.1　行列とベクトルの積で表現できる関数
        4.10.2　定義と簡単な例
        4.10.3　線形関数とゼロベクトル
        4.10.4　線形関数による直線の変換
        4.10.5　単射な線形関数
        4.10.6　全射な線形関数
        4.10.7　FCからFRへの線形関数の行列による表現
        4.10.8　対角行列
    4.11　行列と行列の積
        4.11.1　行列と行列の積の行列とベクトルの積及びベクトルと行列の積による表現
        4.11.2　グラフ、隣接行列、そして道の数え上げ
        4.11.3　行列と行列の積と関数の合成
        4.11.4　行列と行列の積の転置
        4.11.5　列ベクトルと行ベクトル
        4.11.6　全てのベクトルは列ベクトルと解釈される
        4.11.7　線形結合の線形結合、再訪
    4.12　内積と外積
        4.12.1　内積
        4.12.2　外積
    4.13　逆関数から逆行列へ
        4.13.1　線形関数の逆関数も線形である
        4.13.2　逆行列
        4.13.3　逆行列の利用
        4.13.4　可逆行列の積は可逆行列である
        4.13.5　逆行列についての補足
    4.14　ラボ：エラー訂正コード
        4.14.1　チェック行列
        4.14.2　生成子行列
        4.14.3　ハミングコード
        4.14.4　復号化
        4.14.5　エラーシンドローム
        4.14.6　エラーの検出
        4.14.7　全てをまとめる
    4.15　ラボ：2次元幾何学における座標変換
        4.15.1　平面上の点の表現
        4.15.2　座標変換
        4.15.3　画像表現
        4.15.4　画像の読み込みと表示
        4.15.5　線形変換
        4.15.6　平行移動
        4.15.7　スケーリング
        4.15.8　回転
        4.15.9　原点以外の点を中心とした回転
        4.15.10　反転
        4.15.11　色の変換
        4.15.12　より一般的な反転
    4.16　確認用の質問
    4.17　問題

5章　基底
    5.1　座標系
        5.1.1　ルネ・デカルトのアイデア
        5.1.2　座標表現
        5.1.3　座標表現及び行列とベクトルの積
    5.2　はじめての非可逆圧縮
        5.2.1　方法1：最も近いスパースベクトルに置き換える
        5.2.2　方法2：画像ベクトルを座標で表現する
        5.2.3　方法3：複合的な方法
    5.3　生成子を探す2つの欲張りなアルゴリズム
        5.3.1　グローアルゴリズム
        5.3.2　シュリンクアルゴリズム
        5.3.3　欲張って失敗する場合
    5.4　最小全域森とGF(2)
        5.4.1　定義
        5.4.2　最小全域森に対するグローアルゴリズムとシュリンクアルゴリズム
        5.4.3　線形代数での最小全域森
    5.5　線形従属性
        5.5.1　余分なベクトルの補題
        5.5.2　線形従属性の定義
        5.5.3　最小全域森における線形従属性
        5.5.4　線形従属、線形独立の性質
        5.5.5　グローアルゴリズムの考察
        5.5.6　シュリンクアルゴリズムの考察
    5.6　基底
        5.6.1　基底の定義
        5.6.2　FDの標準基底
        5.6.3　全てのベクトル空間が基底を持つことの証明への準備
        5.6.4　ベクトルの有限集合は全てその線形包の基底を含むということ
        5.6.5　Vの任意の線形独立なベクトルの部分集合はVの基底の形にすることができるか？
    5.7　一意的な表現
        5.7.1　基底による座標表現の一意性
    5.8　はじめての基底の変換
        5.8.1　表現からベクトルへの関数
        5.8.2　ある表現から別の表現へ
    5.9　遠近法によるレンダリング
        5.9.1　3次元空間内の点
        5.9.2　カメラと画像平面
        5.9.3　カメラ座標系
        5.9.4　3次元空間内のある点のカメラ座標から対応する画像平面上の点のカメラ座標へ
        5.9.5　3次元空間内の座標からカメラ座標へ
        5.9.6　ピクセル座標系へ
    5.10　基底を求める計算問題
    5.11　交換の補題
        5.11.1　交換の補題
        5.11.2　最小全域森に対するグローアルゴリズムの正当性の証明
    5.12　ラボ：透視補正
        5.12.1　カメラ基底
        5.12.2　ホワイトボード基底
        5.12.3　ピクセルからホワイトボード上の点への写像
        5.12.4　ホワイトボード上にない点から対応するホワイトボードの上の点への写像
        5.12.5　基底の変換行列
        5.12.6　基底の変換行列の計算
        5.12.7　画像表現
        5.12.8　透視補正した画像の生成
    5.13　確認用の質問
    5.14　問題

6章　次元
    6.1　基底ベクトルの個数
        6.1.1　モーフィングの補題とその結果
        6.1.2　モーフィングの補題の証明
    6.2　次元とランク
        6.2.1　定義と例
        6.2.2　幾何学
        6.2.3　グラフの次元とランク
        6.2.4　GF(2)上のベクトル空間の濃度
        6.2.5　Vに属する任意の線形独立なベクトルの集合からVの基底への拡張
        6.2.6　次元原理
        6.2.7　グローアルゴリズムの終了
        6.2.8　ランク定理
        6.2.9　簡単な認証、再訪
    6.3　直和
        6.3.1　定義
        6.3.2　直和の生成子
        6.3.3　直和の基底
        6.3.4　ベクトルの分解の一意性
        6.3.5　補空間
    6.4　次元と線形関数
        6.4.1　線形関数の可逆性
        6.4.2　可逆な最大部分関数
        6.4.3　次元定理
        6.4.4　線形関数の可逆性、再訪
        6.4.5　ランクと退化次数の定理
        6.4.6　チェックサム問題、再訪
        6.4.7　行列の可逆性
        6.4.8　行列の可逆性と基底の変換
    6.5　アニヒレーター
        6.5.1　表現の間の変換
        6.5.2　ベクトル空間のアニヒレーター
        6.5.3　アニヒレーター次元定理
        6.5.4　Vの生成子からVoの生成子へ、及びその逆
        6.5.5　アニヒレーター定理
    6.6　確認用の質問
    6.7　問題

7章　ガウスの掃き出し法
    7.1　階段形式
        7.1.1　階段形式から行ベクトル空間の基底へ
        7.1.2　階段形式における行ベクトルのリスト
        7.1.3　行を0でない要素がはじめて現れる位置でソートする
        7.1.4　行基本変形
        7.1.5　行基本行列を掛ける
        7.1.6　行基本変形による行ベクトル空間の保存
        7.1.7　ガウスの掃き出し法を通じた基底、ランク、そして線形独立性
        7.1.8　ガウスの掃き出し法が失敗する場合
        7.1.9　ピボット化と数値解析
        7.1.10　GF(2)上におけるガウスの掃き出し法
    7.2　ガウスの掃き出し法の他の応用
        7.2.1　逆行列を持つ行列MでMAが階段形式になるものが存在すること
        7.2.2　行列の積を用いずにMを計算する
    7.3　ガウスの掃き出し法による行列とベクトルの方程式の解法
        7.3.1　行列が階段形式の場合の行列とベクトルの方程式の解法..逆行列を持つ場合
        7.3.2　ゼロ行を処理する
        7.3.3　無関係な列を処理する
        7.3.4　単純な認証方式への攻撃とその改善
    7.4　ヌル空間の基底を見つける
    7.5　整数の素因数分解
        7.5.1　素因数分解へのはじめての試み
    7.6　ラボ：閾値シークレットシェアリング
        7.6.1　最初の試み
        7.6.2　うまくいく方法
        7.6.3　本手法の実装
        7.6.4　uの生成
        7.6.5　条件を満たすベクトルの探索
        7.6.6　文字列の共有
    7.7　ラボ：整数の素因数分解
        7.7.1　平方根を用いた最初の試み
        7.7.2　最大公約数を求めるためのユークリッドの互除法
        7.7.3　平方根を用いた試み、再訪
    7.8　確認用の質問
    7.9　問題

8章　内積
    8.1　消防車問題
        8.1.1　距離、長さ、ノルム、内積
    8.2　実数上のベクトルの内積
        8.2.1　実数上のベクトルのノルム
    8.3　直交性
        8.3.1　直交性が満たす性質
        8.3.2　ベクトルbの平行成分と直交成分への分解
        8.3.3　直交性が持つ性質と消防車問題の解
        8.3.4　射影と最も近い点の探索
        8.3.5　消防車問題の解
        8.3.6　*外積と射影
        8.3.7　高次元版の問題の解法に向けて
    8.4　ラボ：機械学習
        8.4.1　データ
        8.4.2　教師あり学習
        8.4.3　仮説クラス
        8.4.4　訓練データにおける誤差を最小化する分類器の選択
        8.4.5　ヒルクライミングによる非線形最適化
        8.4.6　勾配
        8.4.7　最急降下法
    8.5　確認用の質問
    8.6　問題

9章　直交化
    9.1　複数のベクトルに直交する射影
        9.1.1　ベクトルの集合に対する直交性
        9.1.2　ベクトル空間への射影とそれに直交する射影
        9.1.3　ベクトルのリストに直交する射影の第一歩
    9.2　互いに直交するベクトルに直交する射影
        9.2.1　project_orthogonalが正しいことの証明
        9.2.2　project_orthogonalの拡張
    9.3　直交する生成子の集合の作成
        9.3.1　プロシージャorthogonalize
        9.3.2　orthogonalizeが正しいことの証明
    9.4　計算問題「ベクトルの線形包の中で最も近い点」を解く
    9.5　直交化の他の問題への応用
        9.5.1　基底の計算
        9.5.2　部分集合から成る基底の計算
        9.5.3　aug_orthogonalize
        9.5.4　丸め誤差がある場合のアルゴリズム
    9.6　直交補空間
        9.6.1　直交補空間の定義
        9.6.2　直交補空間と直和
        9.6.3　線形包またはアフィン包で与えられたR3における平面に対する法ベクトル
        9.6.4　直交補空間、ヌル空間、アニヒレーター
        9.6.5　方程式で与えられたR3の中の平面に対する法ベクトル
        9.6.6　直交補空間の計算
    9.7　QR分解
        9.7.1　直交行列と列直交行列
        9.7.2　列直交行列の積はノルムを保存する
        9.7.3　行列のQR分解の定義
        9.7.4　Aが線形独立な列ベクトルを持つための条件
    9.8　QR分解による行列の方程式Ax = bの解法
        9.8.1　正方行列の場合
        9.8.2　正方行列の場合の正しさ
        9.8.3　最小二乗問題
        9.8.4　列直交行列の列ベクトルによる座標表現
        9.8.5　Aの行が列より長い場合のQR_solveの使用
    9.9　最小二乗法の応用
        9.9.1　線形回帰（直線へのフィッティング）
        9.9.2　放物線へのフィッティング
        9.9.3　2変数の放物線へのフィッティング
        9.9.4　産業スパイ問題の近似値への応用
        9.9.5　センサーノード問題の近似値への応用
        9.9.6　機械学習の問題への最小二乗法の利用
    9.10　確認用の質問
    9.11　問題

10章　特別な基底
    10.1　最も近いkスパースベクトル
    10.2　与えられた基底に対する表現がkスパースであるような最も近いベクトル
        10.2.1　正規直交基底による座標表現を求める
    10.3　ウェーブレット
        10.3.1　解像度の異なる1次元「画像」
        10.3.2　Vnの直和への分解
        10.3.3　ハールウェーブレット基底
        10.3.4　V1の基底
        10.3.5　一般のnについて
        10.3.6　ウェーブレット変換の最初のステップ
        10.3.7　ウェーブレット分解の以降のステップ
        10.3.8　正規化
        10.3.9　逆変換
        10.3.10　実装
    10.4　多項式の評価と補間
    10.5　フーリエ変換
    10.6　離散フーリエ変換
        10.6.1　指数法則
        10.6.2　n個のストップウォッチ
        10.6.3　離散フーリエ空間：基底関数のサンプリング
        10.6.4　フーリエ行列の逆行列
        10.6.5　高速フーリエ変換（FFT）アルゴリズム
        10.6.6　FFTの導出
        10.6.7　FFTのコーディング
    10.7　複素数上のベクトルの内積
    10.8　巡回行列
        10.8.1　巡回行列とフーリエ行列の列の積
        10.8.2　巡回行列と基底の変換
    10.9　ラボ：ウェーブレットを用いた圧縮
        10.9.1　正規化されていない順変換
        10.9.2　順変換の正規化
        10.9.3　抑制による圧縮
        10.9.4　非正規化
        10.9.5　正規化されていない逆変換
        10.9.6　逆変換
    10.10　2次元画像の処理
        10.10.1　補助プロシージャ
        10.10.2　2次元ウェーブレット変換
        10.10.3　2次元順変換
        10.10.4　いくつかの補助プロシージャ
        10.10.5　2次元逆変換
        10.10.6　画像圧縮の実験
    10.11　確認用の質問
    10.12　問題

11章　特異値分解
    11.1　低ランク行列による行列の近似
        11.1.1　低ランク行列の利点
        11.1.2　行列のノルム
    11.2　路面電車の路線配置問題
        11.2.1　路面電車の路線配置問題の解
        11.2.2　行列のランク1近似
        11.2.3　最適なランク1近似
        11.2.4　最適なランク1近似の表現
        11.2.5　最も近い1次元アフィン空間
    11.3　最も近いk次元ベクトル空間
        11.3.1　特異値と特異ベクトルを求めるための「思考実験的」アルゴリズム
        11.3.2　特異値と右特異ベクトルの性質
        11.3.3　特異値分解
        11.3.4　右特異ベクトルを用いた最も近いk次元空間の求め方
        11.3.5　Aの最適なランクk近似
        11.3.6　最適なランクk近似の行列による表現
        11.3.7　0でない特異値の数とrank Aとの一致
        11.3.8　数値的なランク
        11.3.9　最も近いk次元アフィン空間
        11.3.10　Uが列直交であることの証明
    11.4　特異値分解の利用
        11.4.1　特異値分解の最小二乗問題への応用
    11.5　主成分分析
    11.6　ラボ：固有顔
    11.7　確認用の質問   55211.8問題

12章　固有ベクトル
    12.1　離散力学過程のモデル化
        12.1.1　2つの利息付きの口座
        12.1.2　フィボナッチ数
    12.2　フィボナッチ行列の対角化
    12.3　固有値と固有ベクトル
        12.3.1　相似と対角化可能性
    12.4　固有ベクトルによる座標表現
    12.5　インターネットワーム
    12.6　固有値の存在
        12.6.1　正定値行列と準正定値行列
        12.6.2　異なる固有値を持つ行列
        12.6.3　対称行列
        12.6.4　上三角行列
        12.6.5　一般の正方行列
    12.7　冪乗法
    12.8　マルコフ連鎖
        12.8.1　人口動態のモデル化
        12.8.2　ランディのモデル化
        12.8.3　マルコフ連鎖の定義
        12.8.4　メモリの取り出しにおける空間の局所性のモデル化
        12.8.5　文書のモデル化：不思議の国のハムレット
        12.8.6　それ以外のもののモデル化
        12.8.7　マルコフ連鎖の定常分布
        12.8.8　定常分布が存在するための十分条件
    12.9　ウェブサーファーのモデル化：ページランク
    12.10　*行列式
        12.10.1　平行四辺形の面積
        12.10.2　超平行体の体積
        12.10.3　平行四辺形を用いた多角形面積の表現
        12.10.4　行列式
        12.10.5　行列式関数を用いた固有値の特性化
    12.11　*いくつかの固有定理の証明
        12.11.1　固有値の存在
        12.11.2　対称行列の対角化
        12.11.3　三角化
    12.12　ラボ：ページランク
        12.12.1　概念の導入
        12.12.2　大きなデータセットの使用
        12.12.3　冪乗法を用いたページランクの実装
        12.12.4　データセット
        12.12.5　検索の処理
        12.12.6　ページランクの偏り
        12.12.7　おまけ：複数単語検索の処理
    12.13　確認用の質問
    12.14　問題

13章　線形計画法
    13.1　規定食の問題
    13.2　規定食の問題を線形計画としてとらえる
    13.3　線形計画法の起源
        13.3.1　用語
        13.3.2　線形計画法の異なる形式
        13.3.3　整数による線形計画法
    13.4　線形計画法の幾何学：多面体と頂点
    13.5　多面体の頂点であるような最適解の存在
    13.6　線形計画法の列挙アルゴリズム
    13.7　線形計画法における双対性入門
    13.8　シンプレックスアルゴリズム
        13.8.1　アルゴリズムの終了方法
        13.8.2　現在の解を表現する
        13.8.3　ピボットステップ
        13.8.4　単純な例
    13.9　頂点を見つける
    13.10　ゲーム理論
        13.10.1　線形計画としての定式化
        13.10.2　ノンゼロサムゲーム
    13.11　ラボ：線形計画法を用いた学習
        13.11.1　訓練データの読み込み
        13.11.2　線形計画の準備
        13.11.3　主制約条件
        13.11.4　非負制約条件
        13.11.5　行列A
        13.11.6　右辺のベクトルb
        13.11.7　目的関数ベクトルc
        13.11.8　これまでの作業の統合
        13.11.9　頂点の探索
        13.11.10　線形計画を解く
        13.11.11　結果の利用
    13.12　圧縮センシング
        13.12.1　より高速にMRI画像を得る
        13.12.2　少年を救うための計算
        13.12.3　前進
    13.13　確認用の質問
    13.14　問題

かなりヘビーな内容の印象だが、ベクトル・行列・テンソルを極めることでディープラーニングの肝を押さえられると感じた。

DL/MLと平行して行列プログラミングも取り組んでいくことにする。

６章 学習に関するテクニック ハイパーパラメータ(hyper-parameter)の検証 『ゼロから作るDeep Learning』

６章　最後に、ハイパーパラメータ(hyper-parameter)の検証について。

ハイパーパラメータは人為的に試行錯誤しながら調整がするので検証が必要である。

しかし、汎化性能を評価するには、最終的に評価するための本番のテストデータが使えない。

そこで、ハイパーパラメータ専用の検証データvalidation dataを訓練データから分離して検証が必要。

次にハイパーパラメータの最適化は以下の手順で行う。

ステップ０：ハイパーパラメータの範囲を10^-3から10^3などの範囲でざっくり指定する
↓
ステップ１：設定された範囲からランダムにサンプリングする
↓
ステップ２：サンプリングされた値で学習し、検証データで認識精度を評価する。ただしエポックは小さく設定しておく。
↓
ステップ３：ステップ１−２を一定回数（１００回など）繰り返し、さらにハイパーパラメータの範囲を狭めていく

以下、ハイパーパラメータの最適化をしていくサンプルコード

# coding: utf-8
import sys, os
sys.path.append(os.pardir)  # 親ディレクトリのファイルをインポートするための設定
import numpy as np
import matplotlib.pyplot as plt
plt.switch_backend('agg')

from dataset.mnist import load_mnist
from common.multi_layer_net import MultiLayerNet
from common.util import shuffle_dataset
from common.trainer import Trainer

(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)

# 高速化のため訓練データの削減
x_train = x_train[:500]
t_train = t_train[:500]

# 検証データの分離
validation_rate = 0.20
validation_num = x_train.shape[0] * validation_rate
x_train, t_train = shuffle_dataset(x_train, t_train)
x_val = x_train[:validation_num]
t_val = t_train[:validation_num]
x_train = x_train[validation_num:]
t_train = t_train[validation_num:]


def __train(lr, weight_decay, epocs=50):
    network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100],
                            output_size=10, weight_decay_lambda=weight_decay)
    trainer = Trainer(network, x_train, t_train, x_val, t_val,
                      epochs=epocs, mini_batch_size=100,
                      optimizer='sgd', optimizer_param={'lr': lr}, verbose=False)
    trainer.train()

    return trainer.test_acc_list, trainer.train_acc_list


# ハイパーパラメータのランダム探索======================================
optimization_trial = 100
results_val = {}
results_train = {}
for _ in range(optimization_trial):
    # 探索したハイパーパラメータの範囲を指定===============
    weight_decay = 10 ** np.random.uniform(-8, -4)
    lr = 10 ** np.random.uniform(-6, -2)
    # ================================================

    val_acc_list, train_acc_list = __train(lr, weight_decay)
    print("val acc:" + str(val_acc_list[-1]) + " | lr:" + str(lr) + ", weight decay:" + str(weight_decay))
    key = "lr:" + str(lr) + ", weight decay:" + str(weight_decay)
    results_val[key] = val_acc_list
    results_train[key] = train_acc_list

# グラフの描画========================================================
print("=========== Hyper-Parameter Optimization Result ===========")
graph_draw_num = 20
col_num = 5
row_num = int(np.ceil(graph_draw_num / col_num))
i = 0

for key, val_acc_list in sorted(results_val.items(), key=lambda x:x[1][-1], reverse=True):
    print("Best-" + str(i+1) + "(val acc:" + str(val_acc_list[-1]) + ") | " + key)

    plt.subplot(row_num, col_num, i+1)
    plt.title("Best-" + str(i+1))
    plt.ylim(0.0, 1.0)
    if i % 5: plt.yticks([])
    plt.xticks([])
    x = np.arange(len(val_acc_list))
    plt.plot(x, val_acc_list)
    plt.plot(x, results_train[key], "--")
    i += 1

    if i >= graph_draw_num:
        break

#plt.show()
plt.savefig('hyperparameter_optimization_save.png')

以下、実行結果とグラフ(検証データ：実線、訓練データ：点線）

=========== Hyper-Parameter Optimization Result ===========
Best-1(val acc:0.77) | lr:0.00757365478878744, weight decay:4.612578587686737e-07
Best-2(val acc:0.76) | lr:0.007433061542623079, weight decay:1.0344933324636203e-07
Best-3(val acc:0.76) | lr:0.0069442614770180554, weight decay:3.5083892101171096e-07
Best-4(val acc:0.76) | lr:0.00786568274411027, weight decay:2.128003163191066e-06
Best-5(val acc:0.76) | lr:0.009977128388270529, weight decay:5.034544517460483e-07
Best-6(val acc:0.75) | lr:0.006651552434409378, weight decay:9.770817734920272e-08
Best-7(val acc:0.72) | lr:0.006787994923710441, weight decay:1.538788471810156e-08
Best-8(val acc:0.69) | lr:0.005309167300473579, weight decay:7.092519614173075e-07
Best-9(val acc:0.65) | lr:0.004171913096880143, weight decay:3.7534502493629925e-07
Best-10(val acc:0.64) | lr:0.0036177186197134006, weight decay:3.419650414313433e-07
Best-11(val acc:0.55) | lr:0.004657623419509241, weight decay:1.3150591635104507e-05
Best-12(val acc:0.45) | lr:0.002600118643665009, weight decay:6.101368606264845e-06
Best-13(val acc:0.42) | lr:0.0014781722372820818, weight decay:6.555096165359242e-07
Best-14(val acc:0.35) | lr:0.00112894903737969, weight decay:6.35129426114411e-08
Best-15(val acc:0.35) | lr:0.001122116867042764, weight decay:2.8146026473082357e-05
Best-16(val acc:0.31) | lr:0.0019504915229014257, weight decay:4.5759839999890385e-08
Best-17(val acc:0.29) | lr:0.001523802348758895, weight decay:1.3898280180637062e-07
Best-18(val acc:0.22) | lr:0.0011058186976594655, weight decay:2.7502587954667702e-08
Best-19(val acc:0.21) | lr:0.0004461535980654127, weight decay:7.17362065696084e-05
Best-20(val acc:0.21) | lr:0.0006365291753190107, weight decay:4.449107159041093e-06

Best-5ぐらいまで順調に学習が進んでいることが分かる。

学習係数lrが0.001から0.01

Weight decay係数が10^-8から10^-6

このように、試行錯誤しながら、最適なハイパーパラメータを人為的に特定していかなければならない。

最後に、６章のまとめ問題

・パラメータの更新方法には、SGD以外に◯◯、◯◯、◯◯、などの手法がある
・重みの初期値の推奨は、「◯◯」や「◯◯」である
・◯◯を用いることで学習を加速でき、初期値に左右されにくい◯◯になる
・過学習を抑制する正則化技術として、◯◯や◯◯がある
・ハイパーパラメータの探索は、◯◯するのが効率的である

６章 学習に関するテクニック 正則化, Weight decay, Dropout 『ゼロから作るDeep Learning』

続いて、正則化について。

過学習overfittingの起きる主な２つの原因

・パラメータを大量に持ち、表現力の高いモデルであること
・訓練データが少ないこと

敢えて過学習させたケースをサンプルコードで確認する

# cat overfit_weight_decay_pre_save.py

# coding: utf-8
import os
import sys

sys.path.append(os.pardir)  # 親ディレクトリのファイルをインポートするための設定
import numpy as np
import matplotlib.pyplot as plt
plt.switch_backend('agg')

from dataset.mnist import load_mnist
from common.multi_layer_net import MultiLayerNet
from common.optimizer import SGD

(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)

# 過学習を再現するために、学習データを削減
x_train = x_train[:300]
t_train = t_train[:300]

weight_decay_lambda = 0
#weight_decay_lambda = 0.1
network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10,
                        weight_decay_lambda=weight_decay_lambda)
optimizer = SGD(lr=0.01)

max_epochs = 201
train_size = x_train.shape[0]
batch_size = 100

train_loss_list = []
train_acc_list = []
test_acc_list = []

iter_per_epoch = max(train_size / batch_size, 1)
epoch_cnt = 0

for i in range(1000000000):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]

    grads = network.gradient(x_batch, t_batch)
    optimizer.update(network.params, grads)

    if i % iter_per_epoch == 0:
        train_acc = network.accuracy(x_train, t_train)
        test_acc = network.accuracy(x_test, t_test)
        train_acc_list.append(train_acc)
        test_acc_list.append(test_acc)

        print("epoch:" + str(epoch_cnt) + ", train acc:" + str(train_acc) + ", test acc:" + str(test_acc))

        epoch_cnt += 1
        if epoch_cnt >= max_epochs:
            break



# 3.グラフの描画==========
markers = {'train': 'o', 'test': 's'}
x = np.arange(max_epochs)
plt.plot(x, train_acc_list, marker='o', label='train', markevery=10)
plt.plot(x, test_acc_list, marker='s', label='test', markevery=10)
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
#plt.show()
plt.savefig('overfit_weight_decay_pre.png')

訓練データの認識精度が100%になり、テストデータと大きく乖離していることが分かる。

そこで過学習抑制のため荷重減衰weight decayという手法を使う。 以下のように正則化の強さをコントールするハイパーパラメータを0.1に変更する

# diff overfit_weight_decay_pre_save.py overfit_weight_decay_save.py
20,21c20,21
< weight_decay_lambda = 0
< #weight_decay_lambda = 0.1
---
> #weight_decay_lambda = 0
> weight_decay_lambda = 0.1
68c68
< plt.savefig('overfit_weight_decay_pre.png')
---
> plt.savefig('overfit_weight_decay.png')

訓練データの認識精度が100%ではなくなり、テストデータとの乖離が小さくなっていることが分かる。

続いて、Dropoutという過学習抑制手法について。

Dropoutとは：ニューロンをランダムに消去しながら学習する手法

以下実行したサンプルコード

# cat overfit_dropout_save.py

# coding: utf-8
import os
import sys
sys.path.append(os.pardir)  # 親ディレクトリのファイルをインポートするための設定
import numpy as np
import matplotlib.pyplot as plt
plt.switch_backend('agg')

from dataset.mnist import load_mnist
from common.multi_layer_net_extend import MultiLayerNetExtend
from common.trainer import Trainer

(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)

# 過学習を再現するために、学習データを削減
x_train = x_train[:300]
t_train = t_train[:300]

use_dropout = True  # Dropoutなしのときの場合はFalseに
dropout_ratio = 0.15
network = MultiLayerNetExtend(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100],
                              output_size=10, use_dropout=use_dropout, dropout_ration=dropout_ratio)
trainer = Trainer(network, x_train, t_train, x_test, t_test,
                  epochs=301, mini_batch_size=100,
                  optimizer='sgd', optimizer_param={'lr': 0.01}, verbose=True)
trainer.train()

train_acc_list, test_acc_list = trainer.test_acc_list, trainer.train_acc_list

# グラフの描画==========
markers = {'train': 'o', 'test': 's'}
x = np.arange(len(train_acc_list))
plt.plot(x, train_acc_list, marker='o', label='train', markevery=10)
plt.plot(x, test_acc_list, marker='s', label='test', markevery=10)
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
#plt.show()
plt.savefig('overfit_dropout.png')

確かに荷重減衰手法と同様に、認識精度の乖離が小さくなった。

６章 学習に関するテクニック Batch Normalization 『ゼロから作るDeep Learning』

６章　学習に関するテクニック『ゼロから作るDeep Learning』

続いて、Batch Normalization

Batch Normalization(Batch Norm)とは：ミニバッチごとに正規化する手法。

メリット：

学習を速く進行させることができる
初期値にそれほど依存しない（初期値にロバスト）
過学習を抑制する

以下さまざまな初期値で比較した、サンプルスクリプト

# cat batch_norm_test_save.py

# coding: utf-8
import sys, os
sys.path.append(os.pardir)  # 親ディレクトリのファイルをインポートするための設定
import numpy as np
import matplotlib.pyplot as plt
plt.switch_backend('agg')

from dataset.mnist import load_mnist
from common.multi_layer_net_extend import MultiLayerNetExtend
from common.optimizer import SGD, Adam

(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)

# 学習データを削減
x_train = x_train[:1000]
t_train = t_train[:1000]

max_epochs = 20
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.01


def __train(weight_init_std):
    bn_network = MultiLayerNetExtend(input_size=784, hidden_size_list=[100, 100, 100, 100, 100], output_size=10,
                                    weight_init_std=weight_init_std, use_batchnorm=True)
    network = MultiLayerNetExtend(input_size=784, hidden_size_list=[100, 100, 100, 100, 100], output_size=10,
                                weight_init_std=weight_init_std)
    optimizer = SGD(lr=learning_rate)

    train_acc_list = []
    bn_train_acc_list = []

    iter_per_epoch = max(train_size / batch_size, 1)
    epoch_cnt = 0

    for i in range(1000000000):
        batch_mask = np.random.choice(train_size, batch_size)
        x_batch = x_train[batch_mask]
        t_batch = t_train[batch_mask]

        for _network in (bn_network, network):
            grads = _network.gradient(x_batch, t_batch)
            optimizer.update(_network.params, grads)

        if i % iter_per_epoch == 0:
            train_acc = network.accuracy(x_train, t_train)
            bn_train_acc = bn_network.accuracy(x_train, t_train)
            train_acc_list.append(train_acc)
            bn_train_acc_list.append(bn_train_acc)

            print("epoch:" + str(epoch_cnt) + " | " + str(train_acc) + " - " + str(bn_train_acc))

            epoch_cnt += 1
            if epoch_cnt >= max_epochs:
                break

    return train_acc_list, bn_train_acc_list


# 3.グラフの描画==========
weight_scale_list = np.logspace(0, -4, num=16)
x = np.arange(max_epochs)

for i, w in enumerate(weight_scale_list):
    print( "============== " + str(i+1) + "/16" + " ==============")
    train_acc_list, bn_train_acc_list = __train(w)

    plt.subplot(4,4,i+1)
    plt.title("W:" + str(w))
    if i == 15:
        plt.plot(x, bn_train_acc_list, label='Batch Normalization', markevery=2)
        plt.plot(x, train_acc_list, linestyle = "--", label='Normal(without BatchNorm)', markevery=2)
    else:
        plt.plot(x, bn_train_acc_list, markevery=2)
        plt.plot(x, train_acc_list, linestyle="--", markevery=2)

    plt.ylim(0, 1.0)
    if i % 4:
        plt.yticks([])
    else:
        plt.ylabel("accuracy")
    if i < 12:
        plt.xticks([])
    else:
        plt.xlabel("epochs")
    plt.legend(loc='lower right')

#plt.show()
plt.savefig('batch_norm_test_save.png')

若干表示が崩れたが、確かに多くの場合Batch Normの方が速く学習が進む。

６章 学習に関するテクニック 推奨される重み初期値 『ゼロから作るDeep Learning』

６章　学習に関するテクニック 『ゼロから作るDeep Learning』

続き。

重みの初期値について。

結論として、重みの初期値をゼロにするのはNG。

重みの対照的な構造を崩し、ランダムな初期値を設定する。

勾配消失gradient vanishing：逆伝播での勾配の値が徐々に小さくなること。

多層NNでは勾配消失が問題になるので、推奨された初期値を使う。

活性化関数にS字カーブ(sigmoid,tanh)を使うなら「Xavierの初期値」

活性化関数にReLUを使うなら「Heの初期値」

以下、比較したサンプルコード

# cat weight_init_compare_save.py


# coding: utf-8
import os
import sys

sys.path.append(os.pardir)  # 親ディレクトリのファイルをインポートするための設定
import numpy as np
import matplotlib.pyplot as plt
plt.switch_backend('agg')

from dataset.mnist import load_mnist
from common.util import smooth_curve
from common.multi_layer_net import MultiLayerNet
from common.optimizer import SGD


# 0:MNISTデータの読み込み==========
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)

train_size = x_train.shape[0]
batch_size = 128
max_iterations = 2000


# 1:実験の設定==========
weight_init_types = {'std=0.01': 0.01, 'Xavier': 'sigmoid', 'He': 'relu'}
optimizer = SGD(lr=0.01)

networks = {}
train_loss = {}
for key, weight_type in weight_init_types.items():
    networks[key] = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100],
                                  output_size=10, weight_init_std=weight_type)
    train_loss[key] = []


# 2:訓練の開始==========
for i in range(max_iterations):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]

    for key in weight_init_types.keys():
        grads = networks[key].gradient(x_batch, t_batch)
        optimizer.update(networks[key].params, grads)

        loss = networks[key].loss(x_batch, t_batch)
        train_loss[key].append(loss)

    if i % 100 == 0:
        print("===========" + "iteration:" + str(i) + "===========")
        for key in weight_init_types.keys():
            loss = networks[key].loss(x_batch, t_batch)
            print(key + ":" + str(loss))

# 3.グラフの描画==========
markers = {'std=0.01': 'o', 'Xavier': 's', 'He': 'D'}
x = np.arange(max_iterations)
for key in weight_init_types.keys():
    plt.plot(x, smooth_curve(train_loss[key]), marker=markers[key], markevery=100, label=key)
plt.xlabel("iterations")
plt.ylabel("loss")
plt.ylim(0, 2.5)
plt.legend()
#plt.show()
plt.savefig('weight_init_compare.png')

確かにXavier,Heの初期値の方が学習の進みが速い。

重みを適当に設定せず、適切な学習が進むように適切に設定する必要がある。

６章 学習に関するテクニック SGDとMomentum, AdaGrad, Adam 『ゼロから作るDeep Learning』

６章　学習に関するテクニック

この章では、NN学習でキーとなるアイデアについて学ぶ。

パラメータの更新
重みの初期値
Batch Normalization
正則化
ハイパーパラメータの検証
まとめ

パラメータの更新について。

最適化optimizationとは：NN学習目的である「損失関数を最小化する最適なパラメータ」を見つける問題を解くこと。

確率的勾配降下法SGDの欠点として、関数の形状が等方向でないと非効率な経路で探索する

class SGD:

    """確率的勾配降下法（Stochastic Gradient Descent）"""

    def __init__(self, lr=0.01):
        self.lr = lr

    def update(self, params, grads):
        for key in params.keys():
            params[key] -= self.lr * grads[key]

欠点を改善するため３つの手法Momentum, AdaGrad, Adamがある。以下、サンプルコード。

# Momentum: 速度概念の導入
class Momentum:

    """Momentum SGD"""

    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None

    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():
                self.v[key] = np.zeros_like(val)

        for key in params.keys():
            self.v[key] = self.momentum*self.v[key] - self.lr*grads[key]
            params[key] += self.v[key]

# AdaGrad: 学習係数の減衰learning rate decayの導入
class AdaGrad:

    """AdaGrad"""

    def __init__(self, lr=0.01):
        self.lr = lr
        self.h = None

    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)

        for key in params.keys():
            self.h[key] += grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)


# RMSProp: AdaGradで更新量が0になる問題に対して指数移動平均を導入
class RMSprop:

    """RMSprop"""

    def __init__(self, lr=0.01, decay_rate = 0.99):
        self.lr = lr
        self.decay_rate = decay_rate
        self.h = None

    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)

        for key in params.keys():
            self.h[key] *= self.decay_rate
            self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)


# Adam: MomentumとAdaGradを融合したような手法
class Adam:

    """Adam (http://arxiv.org/abs/1412.6980v8)"""

    def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
        self.lr = lr
        self.beta1 = beta1
        self.beta2 = beta2
        self.iter = 0
        self.m = None
        self.v = None

    def update(self, params, grads):
        if self.m is None:
            self.m, self.v = {}, {}
            for key, val in params.items():
                self.m[key] = np.zeros_like(val)
                self.v[key] = np.zeros_like(val)

        self.iter += 1
        lr_t  = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)

        for key in params.keys():
            #self.m[key] = self.beta1*self.m[key] + (1-self.beta1)*grads[key]
            #self.v[key] = self.beta2*self.v[key] + (1-self.beta2)*(grads[key]**2)
            self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
            self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])

            params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)

            #unbias_m += (1 - self.beta1) * (grads[key] - self.m[key]) # correct bias
            #unbisa_b += (1 - self.beta2) * (grads[key]*grads[key] - self.v[key]) # correct bias
            #params[key] += self.lr * unbias_m / (np.sqrt(unbisa_b) + 1e-7)

続いて、SGD, Momentum, AdaGrad, Adamの比較

# coding: utf-8
import os
import sys
sys.path.append(os.pardir)  # 親ディレクトリのファイルをインポートするための設定
import matplotlib.pyplot as plt
plt.switch_backend('agg')
from dataset.mnist import load_mnist
from common.util import smooth_curve
from common.multi_layer_net import MultiLayerNet
from common.optimizer import *


# 0:MNISTデータの読み込み==========
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)

train_size = x_train.shape[0]
batch_size = 128
max_iterations = 2000


# 1:実験の設定==========
optimizers = {}
optimizers['SGD'] = SGD()
optimizers['Momentum'] = Momentum()
optimizers['AdaGrad'] = AdaGrad()
optimizers['Adam'] = Adam()
#optimizers['RMSprop'] = RMSprop()

networks = {}
train_loss = {}
for key in optimizers.keys():
    networks[key] = MultiLayerNet(
        input_size=784, hidden_size_list=[100, 100, 100, 100],
        output_size=10)
    train_loss[key] = []

# 2:訓練の開始==========
for i in range(max_iterations):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]

    for key in optimizers.keys():
        grads = networks[key].gradient(x_batch, t_batch)
        optimizers[key].update(networks[key].params, grads)

        loss = networks[key].loss(x_batch, t_batch)
        train_loss[key].append(loss)

    if i % 100 == 0:
        print( "===========" + "iteration:" + str(i) + "===========")
        for key in optimizers.keys():
            loss = networks[key].loss(x_batch, t_batch)
            print(key + ":" + str(loss))


# 3.グラフの描画==========
markers = {"SGD": "o", "Momentum": "x", "AdaGrad": "s", "Adam": "D"}
x = np.arange(max_iterations)
for key in optimizers.keys():
    plt.plot(x, smooth_curve(train_loss[key]), marker=markers[key], markevery=100, label=key)
plt.xlabel("iterations")
plt.ylabel("loss")
plt.ylim(0, 1)
plt.legend()
#plt.show()
plt.savefig('optimizer_compare_mnist.png')

確かにSGDより優れた手法であることが分かった。

以下、続く。

重みの初期値 Batch Normalization 正則化 ハイパーパラメータの検証 まとめ

5章 誤差逆伝播法（ごさぎゃくでんぱほう）Backpropagation『ゼロから作るDeep Learning』

5章誤差逆伝播法

いよいよ誤差逆伝播法まできた。

数式より計算グラフの方が理解しやすいらしい。

詳しくは本書参照。

まずはレイヤ概念の導入。

レイヤ(層)とは：NNにおける機能の単位を指す。レイヤ単位で実装することで、ブロックのように積み上げていける。

まず、乗算レイヤの実装と、加算レイヤの実装について。

# cat layer_naive.py


# coding: utf-8


class MulLayer:
    def __init__(self):
        self.x = None
        self.y = None

    def forward(self, x, y):
        self.x = x
        self.y = y
        out = x * y

        return out

    def backward(self, dout): #dout微分
        dx = dout * self.y
        dy = dout * self.x

        return dx, dy


class AddLayer:
    def __init__(self):
        pass

    def forward(self, x, y):
        out = x + y

        return out

    def backward(self, dout):
        dx = dout * 1
        dy = dout * 1

        return dx, dy

つぎに、活性化関数レイヤ(ReLUレイヤ、Sigmoidレイヤ)の実装について。

# cat common/layers.py

# coding: utf-8
import numpy as np
from common.functions import *
from common.util import im2col, col2im


class Relu:
    def __init__(self):
        self.mask = None

    def forward(self, x):
        self.mask = (x <= 0)
        out = x.copy()
        out[self.mask] = 0

        return out

    def backward(self, dout):
        dout[self.mask] = 0
        dx = dout

        return dx


class Sigmoid:
    def __init__(self):
        self.out = None

    def forward(self, x):
        out = sigmoid(x)
        self.out = out
        return out

    def backward(self, dout):
        dx = dout * (1.0 - self.out) * self.out

        return dx

つぎに、Affineレイヤの実装について。

Affineとは：行列の内積を行うレイヤ。幾何学で「アフィン変換」と呼ばれる。

class Affine:
    def __init__(self, W, b):
        self.W =W
        self.b = b

        self.x = None
        self.original_x_shape = None
        # 重み・バイアスパラメータの微分
        self.dW = None
        self.db = None

    def forward(self, x):
        # テンソル対応
        self.original_x_shape = x.shape
        x = x.reshape(x.shape[0], -1)
        self.x = x

        out = np.dot(self.x, self.W) + self.b

        return out

    def backward(self, dout):
        dx = np.dot(dout, self.W.T)
        self.dW = np.dot(self.x.T, dout)
        self.db = np.sum(dout, axis=0)

        dx = dx.reshape(*self.original_x_shape)  # 入力データの形状に戻す（テンソル対応）
        return dx

つぎに、Softmaxレイヤの実装について。

Softmaxレイヤは学習時のみ必要で推論時には必要ない。

サンプルでは、Softmax関数と交差エントロピー誤差のレイヤSoftmax-with-Lossを定義している

導出過程が複雑なので、付録Aをあとで参照。

class SoftmaxWithLoss:
    def __init__(self):
        self.loss = None
        self.y = None # softmaxの出力
        self.t = None # 教師データ

    def forward(self, x, t):
        self.t = t
        self.y = softmax(x)
        self.loss = cross_entropy_error(self.y, self.t)

        return self.loss

    def backward(self, dout=1):
        batch_size = self.t.shape[0]
        if self.t.size == self.y.size: # 教師データがone-hot-vectorの場合
            dx = (self.y - self.t) / batch_size
        else:
            dx = self.y.copy()
            dx[np.arange(batch_size), self.t] -= 1
            dx = dx / batch_size

        return dx

最後に、誤差逆伝播法の実装について。

以下の学習4ステップのうち、ステップ2勾配の算出で登場

学習の４ステップ

ステップ１ミニバッチ：ミニバッチをランダムに選択
ステップ２勾配算出：ミニバッチの損失関数を減らす勾配を算出
ステップ３パラメータ更新：重みパラメータを勾配方向に微小量だけ更新
ステップ４反復：ステップ１−３を反復

# cat two_layer_net.py


# coding: utf-8
import sys, os
sys.path.append(os.pardir)  # 親ディレクトリのファイルをインポートするための設定
import numpy as np
from common.layers import *
from common.gradient import numerical_gradient
from collections import OrderedDict


class TwoLayerNet:

    def __init__(self, input_size, hidden_size, output_size, weight_init_std = 0.01):
        # 重みの初期化
        self.params = {}
        self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
        self.params['b1'] = np.zeros(hidden_size)
        self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
        self.params['b2'] = np.zeros(output_size)

        # レイヤの生成
        self.layers = OrderedDict()
        self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1'])
        self.layers['Relu1'] = Relu()
        self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2'])

        self.lastLayer = SoftmaxWithLoss()

    def predict(self, x):
        for layer in self.layers.values():
            x = layer.forward(x)

        return x

    # x:入力データ, t:教師データ
    def loss(self, x, t):
        y = self.predict(x)
        return self.lastLayer.forward(y, t)

    def accuracy(self, x, t):
        y = self.predict(x)
        y = np.argmax(y, axis=1)
        if t.ndim != 1 : t = np.argmax(t, axis=1)

        accuracy = np.sum(y == t) / float(x.shape[0])
        return accuracy

    # x:入力データ, t:教師データ
    def numerical_gradient(self, x, t):
        loss_W = lambda W: self.loss(x, t)

        grads = {}
        grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
        grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
        grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
        grads['b2'] = numerical_gradient(loss_W, self.params['b2'])

        return grads

    def gradient(self, x, t):
        # forward
        self.loss(x, t)

        # backward
        dout = 1
        dout = self.lastLayer.backward(dout)

        layers = list(self.layers.values())
        layers.reverse()
        for layer in layers:
            dout = layer.backward(dout)

        # 設定
        grads = {}
        grads['W1'], grads['b1'] = self.layers['Affine1'].dW, self.layers['Affine1'].db
        grads['W2'], grads['b2'] = self.layers['Affine2'].dW, self.layers['Affine2'].db

        return grads

実装した誤差逆伝播法の勾配確認をおこなう。

勾配確認gradient checkとは：誤差逆伝播法と数値微分の結果を比較し、ほぼ近似できることで誤差逆伝播法の正しさを確認すること。

# cat deep-learning-from-scratch/ch05/gradient_check.py
# coding: utf-8
import sys, os
sys.path.append(os.pardir)  # 親ディレクトリのファイルをインポートするための設定
import numpy as np
from dataset.mnist import load_mnist
from two_layer_net import TwoLayerNet

# データの読み込み
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)

network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)

x_batch = x_train[:3]
t_batch = t_train[:3]

grad_numerical = network.numerical_gradient(x_batch, t_batch)
grad_backprop = network.gradient(x_batch, t_batch)

for key in grad_numerical.keys():
    diff = np.average( np.abs(grad_backprop[key] - grad_numerical[key]) )
    print(key + ":" + str(diff))

勾配確認のサンプルコードを実行してみる：

# py gradient_check.py
W2:9.77654477536e-13
W1:2.37797639143e-13
b2:1.2012613404e-10
b1:7.43019632366e-13

ほぼ誤差がないことが分かった。

そして、誤差逆伝播法を訓練データを学習させてみる。

# py train_neuralnet.py

0.102266666667 0.1016
0.90125 0.9073
0.9205 0.9221
0.936033333333 0.9349
0.945816666667 0.9461
0.9512 0.9504
0.957433333333 0.955
0.961133333333 0.959
0.965266666667 0.962
0.967566666667 0.9636
0.970366666667 0.9637
0.97065 0.9635
0.974466666667 0.9674
0.974416666667 0.9671
0.976816666667 0.968
0.97775 0.9698
0.978783333333 0.971

認識精度がかなり向上していることがわかる。

5章まとめ問題

・◯◯1を用いれば計算過程を視覚的に把握できる
・◯◯2は局所的な計算によって全体の計算を構成する
・◯◯1の◯◯3は通常の計算を行い、◯◯4によって各ノードの微分が求まる
・◯◯5とは、NNの構成要素を◯◯6で実装することで勾配計算を効率化する
・◯◯6とは、◯◯5と◯◯7の結果を比較して◯◯5の実装が誤っていないことが確認できる

ニューラルネットワークを図解するためグラフ描画ツールgraphviz導入

こんな感じのグラフがスクリプトで作成できるgraphviz

以下、ギャラリー。

Gallery | Graphviz - Graph Visualization Software

まずは、インストール。

# まずは、Anacondaでgraphvizパッケージをインストール
conda install -c anaconda graphviz=2.38.0
# が、importできず、改めてpipで入れなおし
pip install graphviz

# 確認
dot -V
dot - graphviz version 2.38.0 (20140413.2041)

次に、dotファイル。

# cat neuralnet.dot


digraph G {

  rankdir=LR
  splines=line
  nodesep=.05;

  node [label=""];

  subgraph cluster_0 {
  color=white;
  node [style=solid,color=blue4, shape=circle];
  x1 [label="x1"];
  x2 [label="x2"];
  label = "input";
  }

  subgraph cluster_1 {
  color=white;
  node [style=solid,color=red2, shape=circle];
  a12 a22 a32;
  label = "layer 2";
  }

  subgraph cluster_2 {
  color=white;
  node [style=solid,color=red2, shape=circle];
  a13 a23;
  label = "layer 3";
  }

  subgraph cluster_3 {
  color=white;
  node [style=solid,color=seagreen2, shape=circle];
  y1 [label="y1"];
  y2 [label="y2"];
  label="output";
  }

  x1 -> a12;
  x1 -> a22;
  x1 -> a32;

  x2 -> a12;
  x2 -> a22;
  x2 -> a32;

  a12 -> a13
  a22 -> a13
  a32 -> a13

  a12 -> a23
  a22 -> a23
  a32 -> a23

  a13 -> y1
  a23 -> y1

  a13 -> y2
  a23 -> y2
}

最後に、画像出力。

# dot -Tpng -O neuralnet.dot

ただ、手元の環境だとなぜかラベルがASCIIなのに文字化けるので、オンライン上で実行できるサービスを探してみると、いろいろある。

http://www.webgraphviz.com/

ただ、ソースを貼って実行するだけ。

一方、こちらは、 HTMLのimageタグにそのままdotファイル内の記述をsrcに指定してやれば画像生成される便利なサービス

http://www.gravizo.com/

こんな感じで指定。面白い。

<img src='http://g.gravizo.com/g?
 digraph G {
   main -> parse -> execute;
   main -> init;
   main -> cleanup;
   execute -> make_string;
   execute -> printf
   init -> make_string;
   main -> printf;
   execute -> compare;
 }
'/>

2〜4章まとめの確認問題『ゼロから作るDeep Learning』

いったん4章までの復習がてら、２・３・４章末まとめから問題を作成してみる。

2章
・パーセプトロンは、ある◯◯を与えたら、決まった◯◯を行うアルゴリズムである。
・パーセプトロンでは、◯◯と◯◯をパラメータとして設定する。
・パーセプトロンを用いれば、◯◯や◯◯ゲートなどの論理回路を表現できる。
・単層パーセプトロンでは◯◯ゲートを表現できないが、2層パーセプトロンなら表現できる。
・単層パーセプトロンでは◯◯領域だけしか表現できないが、二層パーセプトロンでは◯◯領域を表現できる。
・多層パーセプトロンは、理論上◯◯を表現できる。


3章
・ニューラルネットワーク(NN)では、活性化関数として、◯◯や◯◯のような滑らかに変化する関数を利用する。
・NumPyの◯◯を上手く使うことでNNを効率良く実装できる。
・機械学習(ML)の問題は、◯◯1問題と◯◯2問題に大別できる。
・出力層で使用する活性化関数は、◯◯1問題では◯◯関数、◯◯2問題では◯◯関数を一般的に利用する。
・◯◯2問題では、出力層のニューロン数を◯◯に設定する。
・入力データのまとまりである◯◯単位で推論処理を行えば、計算が高速化する。


4章
・MLで使用するデータセットは、◯◯1データと◯◯2データに分けて使用する。
・◯◯1データで学習を行い、◯◯能力を◯◯2データで評価する。
・NNの学習は、◯◯を指標とし、◯◯の値が小さくなるように◯◯3を更新する。
・◯◯3を更新する際には、◯◯3の◯◯を利用して、◯◯方向に◯◯を更新する作業を繰り返す。
・微小な値を与えたときの差分によって微分を求めることを◯◯4という。
・◯◯4によって、◯◯を求めることができる。
・◯◯4の計算は低速だが実装は簡単である一方、◯◯の実装は複雑だが高速に◯◯を求められる。

3章辺りから理解曲線勾配の上昇率が高くなってきてキツいが、３歩進んで2歩下がっても、理論上最終ゴールに到達できるのでコツコツ進む。

4章ニューラルネットワークの学習 学習アルゴリズムの実装『ゼロから作るDeep Learning』

4章続き。 学習アルゴリズムの実装

改めて学習とは：適応可能な重みとバイアスを訓練データに適応するように調整すること

学習の４ステップ

ステップ１：ミニバッチをランダムに選択
ステップ２：ミニバッチの損失関数を減らす勾配を算出
ステップ３：重みパラメータを勾配方向に微小量だけ更新
ステップ４：ステップ１−３を反復

ミニバッチをランダム選択することから、
確率的勾配下降法(SGD, stochastic gradient descent)と呼ぶ。

２層ニューラルネットワークのクラスプログラムを参照。今までの総まとめ。

# cat two_layer_net.py


# coding: utf-8
import sys, os
sys.path.append(os.pardir)  # 親ディレクトリのファイルをインポートするための設定
from common.functions import *
from common.gradient import numerical_gradient


class TwoLayerNet:

    def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
        # 重みの初期化
        self.params = {}
        self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
        self.params['b1'] = np.zeros(hidden_size)
        self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
        self.params['b2'] = np.zeros(output_size)

    def predict(self, x):
        W1, W2 = self.params['W1'], self.params['W2']
        b1, b2 = self.params['b1'], self.params['b2']

        a1 = np.dot(x, W1) + b1
        z1 = sigmoid(a1)
        a2 = np.dot(z1, W2) + b2
        y = softmax(a2)

        return y

    # x:入力データ, t:教師データ
    def loss(self, x, t):
        y = self.predict(x)

        return cross_entropy_error(y, t)

    def accuracy(self, x, t):
        y = self.predict(x)
        y = np.argmax(y, axis=1)
        t = np.argmax(t, axis=1)

        accuracy = np.sum(y == t) / float(x.shape[0])
        return accuracy

    # x:入力データ, t:教師データ
    def numerical_gradient(self, x, t):
        loss_W = lambda W: self.loss(x, t)

        grads = {}
        grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
        grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
        grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
        grads['b2'] = numerical_gradient(loss_W, self.params['b2'])

        return grads

    def gradient(self, x, t):
        W1, W2 = self.params['W1'], self.params['W2']
        b1, b2 = self.params['b1'], self.params['b2']
        grads = {}

        batch_num = x.shape[0]

        # forward
        a1 = np.dot(x, W1) + b1
        z1 = sigmoid(a1)
        a2 = np.dot(z1, W2) + b2
        y = softmax(a2)

        # backward
        dy = (y - t) / batch_num
        grads['W2'] = np.dot(z1.T, dy)
        grads['b2'] = np.sum(dy, axis=0)

        da1 = np.dot(dy, W2.T)
        dz1 = sigmoid_grad(a1) * da1
        grads['W1'] = np.dot(x.T, dz1)
        grads['b1'] = np.sum(dz1, axis=0)

        return grads

そして、バッチサイズ100を10000回SGDでパラメータ更新するサンプルプログラム

# cat train_neuralnet_save.py

# coding: utf-8
import sys, os
sys.path.append(os.pardir)  # 親ディレクトリのファイルをインポートするための設定
import numpy as np
import matplotlib.pyplot as plt
plt.switch_backend('agg')
from dataset.mnist import load_mnist
from two_layer_net import TwoLayerNet

# データの読み込み
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)

network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)

iters_num = 10000  # 繰り返しの回数を適宜設定する
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1

train_loss_list = []
train_acc_list = []
test_acc_list = []

iter_per_epoch = max(train_size / batch_size, 1)

for i in range(iters_num):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]

    # 勾配の計算
    #grad = network.numerical_gradient(x_batch, t_batch)
    grad = network.gradient(x_batch, t_batch)

    # パラメータの更新
    for key in ('W1', 'b1', 'W2', 'b2'):
        network.params[key] -= learning_rate * grad[key]

    loss = network.loss(x_batch, t_batch)
    train_loss_list.append(loss)

    if i % iter_per_epoch == 0:
        train_acc = network.accuracy(x_train, t_train)
        test_acc = network.accuracy(x_test, t_test)
        train_acc_list.append(train_acc)
        test_acc_list.append(test_acc)
        print("train acc, test acc | " + str(train_acc) + ", " + str(test_acc))

# グラフの描画
markers = {'train': 'o', 'test': 's'}
x = np.arange(len(train_acc_list))
plt.plot(x, train_acc_list, label='train acc')
plt.plot(x, test_acc_list, label='test acc', linestyle='--')
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
#plt.show()
plt.savefig('train_neuralnet.png')

そして、実行結果。1エポックごとの認識精度が向上していることがわかる。

# py train_neuralnet_save.py
train acc, test acc | 0.0987166666667, 0.098
train acc, test acc | 0.788433333333, 0.7953
train acc, test acc | 0.874716666667, 0.8796
train acc, test acc | 0.898033333333, 0.9014
train acc, test acc | 0.9083, 0.9109
train acc, test acc | 0.9141, 0.9171
train acc, test acc | 0.919933333333, 0.9215
train acc, test acc | 0.924516666667, 0.9264
train acc, test acc | 0.927233333333, 0.9293
train acc, test acc | 0.930866666667, 0.9316
train acc, test acc | 0.93405, 0.9344
train acc, test acc | 0.937083333333, 0.9367
train acc, test acc | 0.93835, 0.9372
train acc, test acc | 0.941066666667, 0.9402
train acc, test acc | 0.94335, 0.9426
train acc, test acc | 0.945, 0.9442
train acc, test acc | 0.946916666667, 0.9459

訓練データとテストデータに差異がほぼないことから過学習が起きていないことも分かった。

4章ニューラルネットワークの学習 数値微分、偏微分、勾配法、学習率『ゼロから作るDeep Learning』

『ゼロから作るDeep Learning』4章続き。

微分とは：ある瞬間の変化量

数値微分numerical differentiationとは：微小な差分によって微分を求めること

def numerical_diff(f, x):
  h = 1e-4 #0.0001程度の値が適当な微小値
  return ( f(x+h) - f(x-h) ) / (2*h)

サンプルコードを改変してグラフを生成してみる

# cat gradient_1d_save.py
# coding: utf-8
import numpy as np
import matplotlib.pylab as plt
plt.switch_backend('agg')


def numerical_diff(f, x):
    h = 1e-4 # 0.0001
    return (f(x+h) - f(x-h)) / (2*h)


def function_1(x):
    return 0.01*x**2 + 0.1*x


def tangent_line(f, x):
    d = numerical_diff(f, x)
    print(d)
    y = f(x) - d*x
    return lambda t: d*t + y

x = np.arange(0.0, 20.0, 0.1)
y = function_1(x)
plt.xlabel("x")
plt.ylabel("f(x)")

tf = tangent_line(function_1, 5) # 5->10に変更すれば2つ目の画像になる
y2 = tf(x)

plt.plot(x, y)
plt.plot(x, y2)
plt.savefig('gradient_1d.png')

続いて、偏微分

偏微分とは：複数の変数からなる関数の微分

x0, x1の2変数関数の定義とグラフを表示

def function_2(x):
  return x[0]**2 + x[1]**2

# 3Dグラフを描画
# cat multivariate_func_save.py
# coding: utf-8
import numpy as np
import matplotlib.pylab as plt
plt.switch_backend('agg')
from mpl_toolkits.mplot3d import Axes3D

x = np.meshgrid(np.arange(-3, 3, 0.1), np.arange(-3, 3, 0.1))
z = x[0]**2 + x[1]**2

fig = plt.figure()
ax = Axes3D(fig)
ax.plot_wireframe(x[0], x[1], z)

plt.xlim(-3.5, 3.5)
plt.ylim(-4.5, 4.5)
plt.xlabel("x0")
plt.ylabel("x1")
plt.savefig('multivariate_func.png')

ところで、Pythonで微分コマンドなどあるのだろうか、と調査するとSympyで数学できるらしいので、さっそく導入

# conda install -c anaconda sympy=1.0
# py
>>> from sympy import *
>>> var('x')
x
>>> diff(sin(x),x)
cos(x)

こちらがドキュメント

Welcome to SymPy’s documentation! — SymPy 1.0 documentation

さて、続いて、勾配。

勾配gradientとは：すべての変数の偏微分をベクトルとしてまとめたもの

# f(x0, x1) = x0**2 + x1**2の勾配図を描くサンプルコード実行

# cat gradient_2d_save.py

# coding: utf-8
# cf.http://d.hatena.ne.jp/white_wheels/20100327/p3
import numpy as np
import matplotlib.pylab as plt
plt.switch_backend('agg')
from mpl_toolkits.mplot3d import Axes3D


def _numerical_gradient_no_batch(f, x):
    h = 1e-4 # 0.0001
    grad = np.zeros_like(x)

    for idx in range(x.size):
        tmp_val = x[idx]
        x[idx] = float(tmp_val) + h
        fxh1 = f(x) # f(x+h)

        x[idx] = tmp_val - h
        fxh2 = f(x) # f(x-h)
        grad[idx] = (fxh1 - fxh2) / (2*h)

        x[idx] = tmp_val # 値を元に戻す

    return grad


def numerical_gradient(f, X):
    if X.ndim == 1:
        return _numerical_gradient_no_batch(f, X)
    else:
        grad = np.zeros_like(X)

        for idx, x in enumerate(X):
            grad[idx] = _numerical_gradient_no_batch(f, x)

        return grad


def function_2(x):
    if x.ndim == 1:
        return np.sum(x**2)
    else:
        return np.sum(x**2, axis=1)


def tangent_line(f, x):
    d = numerical_gradient(f, x)
    print(d)
    y = f(x) - d*x
    return lambda t: d*t + y

if __name__ == '__main__':
    x0 = np.arange(-2, 2.5, 0.25)
    x1 = np.arange(-2, 2.5, 0.25)
    X, Y = np.meshgrid(x0, x1)

    X = X.flatten()
    Y = Y.flatten()

    grad = numerical_gradient(function_2, np.array([X, Y]) )

    plt.figure()
    plt.quiver(X, Y, -grad[0], -grad[1],  angles="xy",color="#666666")#,headwidth=10,scale=40,color="#444444")
    plt.xlim([-2, 2])
    plt.ylim([-2, 2])
    plt.xlabel('x0')
    plt.ylabel('x1')
    plt.grid()
    plt.legend()
    plt.draw()
    #plt.show()
    plt.savefig('gradient_2d.png')

確かに3Dグラフの谷に向かってベクトルが向いている

次に、勾配法。

勾配法gradient methodとは：現在の場所から勾配方向に一定距離だけ進み、移動先でも同様に繰り返し勾配方向へ移動することで関数の値を徐々に減らす方法

勾配降下法gradient descent methodとは：最小値を探す勾配法で、ニューラルネットワークの分野で使われる

学習率learning rateとは：一回の学習でどれだけ学習しパラメータを更新するのかを決める割合。大きすぎても小さすぎても最適化できないので調整・確認が必要。

ハイパーパラメータhyperparameterとは：学習率のように、ニューラルネットワークのパラメータとは性質の異なる人為設定するパラメータ。

以下勾配法で最小値を探索するサンプルコード

# cat gradient_method_save.py
# coding: utf-8
import numpy as np
import matplotlib.pylab as plt
plt.switch_backend('agg')
from gradient_2d import numerical_gradient


def gradient_descent(f, init_x, lr=0.01, step_num=100):
    x = init_x
    x_history = []

    for i in range(step_num):
        x_history.append( x.copy() )

        grad = numerical_gradient(f, x)
        x -= lr * grad

    return x, np.array(x_history)


def function_2(x):
    return x[0]**2 + x[1]**2

init_x = np.array([-3.0, 4.0])

lr = 0.1
step_num = 20
x, x_history = gradient_descent(function_2, init_x, lr=lr, step_num=step_num)

plt.plot( [-5, 5], [0,0], '--b')
plt.plot( [0,0], [-5, 5], '--b')
plt.plot(x_history[:,0], x_history[:,1], 'o')

plt.xlim(-3.5, 3.5)
plt.ylim(-4.5, 4.5)
plt.xlabel("X0")
plt.ylabel("X1")
#plt.show()
plt.savefig('gradient_method.png')

最後にニューラルネットワークの勾配を求めるサンプルコード

# coding: utf-8
import sys, os
sys.path.append(os.pardir)  # 親ディレクトリのファイルをインポートするための設定
import numpy as np
from common.functions import softmax, cross_entropy_error
from common.gradient import numerical_gradient


class simpleNet:
    def __init__(self):
        self.W = np.random.rand(2,3)

    def predict(self, x):
        return np.dot(x, self.W)

    def loss(self, x, t):
        z = self.predict(x)
        y = softmax(z)
        loss = cross_entropy_error(y, t)

        return loss

x = np.random.rand(2)
t = np.array([0,0,1])

net = simpleNet()

f = lambda w: net.loss(x, t)
dW = numerical_gradient(f, net.W)

print(dW)

4章ニューラルネットワークの学習 データ駆動アプローチ、損失関数、ミニバッチ『ゼロから作るDeep Learning』

3章ではニューラルネットワークの「推論」を実装したが、4章からニューラルネットワークの「学習」を実装する。

「学習」とは：訓練データから最適な重みパラメータ値を自動で獲得すること

パラメータの数は、実際数千〜数億にも及ぶため、手動で調整することは不可能

「データ駆動アプローチ」：いままでの「人」を中心としたアプローチではなく、「データ」を中心としたアプローチ

ニューラルネットワークやディープラーニングでは、従来の機械学習以上に、属人性を排している

・機械学習(ML)以前　入力データ　→　人力処理　→　出力データ
↓
・ML　入力データ　→　人力特徴量　→　ML自動処理　→　出力データ
↓
・NNやDL　入力データ　→　NN/DL自動処理　→　出力データ

機械学習におけるデータの取扱について

2種類のデータ：「訓練(教師)データ」と「テストデータ」

まず「訓練(教師)データ」で学習し、最適なパラメータを探索

つぎに「テストデータ」で汎化能力を評価し、一部のデータセットだけ過度に対応した「過学習overfitting」を避ける

「損失関数loss function」：ニューラルネットワークの学習で用いられる指標で、主に「二乗和誤差」「交差エントロピー誤差」が用いられる

「二乗和誤差」について。

# 二乗和誤差
def mean_squared_error(y, t): #y: ニューラルネットワークの出力、t:訓練データ
  return np.sum( (y - t)**2 ) / 2

# 実行例
# cat mean_squared_error.py
#!/usr/bin/env python

import numpy as np
import my_module as my

# 訓練データ(「2」を正解とするone-hot表現
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]

# 例1: '2'の確率が最も高い場合
y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
print(np.sum(y)) #=> 1.0

y = my.mean_squared_error(np.array(y), np.array(t))
print(y) #=> 0.0975

# 例2: '7'の確率が最も高い場合
y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
print(np.sum(y)) #=> 1.0

y = my.mean_squared_error(np.array(y), np.array(t))
print(y) #=> 0.5975

「交差エントロピー誤差」について。

#交差エントロピー誤差
def cross_entropy_error(y, t):
  delta = 1e-7 # マイナス無限大を回避するための微小値
  return - np.sum( t * np.log( y + delta ) )


# 実行例
# cat cross_entropy_error.py
#!/usr/bin/env python

import numpy as np
import my_module as my

# 訓練データ(「2」を正解とするone-hot表現
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]

# 例1: '2'の確率が最も高い場合
y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
print(np.sum(y)) #=> 1.0

y = my.cross_entropy_error(np.array(y), np.array(t))
print(y) #=> 0.510825457099

# 例2: '7'の確率が最も高い場合
y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
print(np.sum(y)) #=> 1.0

y = my.cross_entropy_error(np.array(y), np.array(t))
print(y) #=> 2.30258409299

続いて、大量にある全データのうち一部を選出して近似とする「ミニバッチ学習」について。

# 0から指定された数字(60000)未満までの数字をランダムに指定個数(10)選択する処理
>>> import numpy as np
>>> np.random.choice(60000, 10)
array([54904, 15528, 35786, 44249, 25077, 37764, 46607,   552, 33463, 12885])
>>> np.random.choice(60000, 10)
array([38745,  8181,  8602, 37811, 24747, 18214, 50371, 13052, 13100, 36289])
>>> np.random.choice(60000, 10)

MNISTデータセットで動作確認

# cat mini_batch.py
# coding: utf-8
import sys, os
sys.path.append(os.pardir)
import numpy as np
from dataset.mnist import load_mnist

(x_train, t_train), (x_test, t_test) = \
  load_mnist(normalize=True, one_hot_label=True)

print(x_train.shape) #=>(60000, 784)
print(t_train.shape) #=>(60000, 10)

# mini_batch
train_size = x_train.shape[0]
batch_size = 10
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]

print(x_batch) #=>ランダム結果
'''
[[ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]
 ...,
 [ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]]
'''

print(t_batch) #=>ランダム結果
'''
[[ 0.  0.  0.  0.  0.  1.  0.  0.  0.  0.]
 [ 0.  0.  0.  0.  0.  0.  0.  1.  0.  0.]
 [ 0.  0.  0.  1.  0.  0.  0.  0.  0.  0.]
 [ 1.  0.  0.  0.  0.  0.  0.  0.  0.  0.]
 [ 1.  0.  0.  0.  0.  0.  0.  0.  0.  0.]
 [ 1.  0.  0.  0.  0.  0.  0.  0.  0.  0.]
 [ 0.  0.  0.  1.  0.  0.  0.  0.  0.  0.]
 [ 0.  0.  0.  0.  0.  0.  0.  0.  0.  1.]
 [ 0.  0.  0.  0.  1.  0.  0.  0.  0.  0.]
 [ 0.  0.  0.  1.  0.  0.  0.  0.  0.  0.]]
'''

交差エントロピー誤差関数の改変

#交差エントロピー誤差(バッチ対応版）
def cross_entropy_error_batch(y, t):
  if y.ndim == 1:
    t = t.reshape(1, t.size)
    y = y.reshape(1, y.size)

  batch_size = y.shape[0]
  return - ( np.sum( t * np.log( y ) ) / batch_size )


#交差エントロピー誤差(バッチ対応、教師データラベル版）
#one-hot表現ではなく'2'などのラベル
def cross_entropy_error_batch_label(y, t):
  if y.ndim == 1:
    t = t.reshape(1, t.size)
    y = y.reshape(1, y.size)

  batch_size = y.shape[0]
  return - ( np.sum( t * np.log( y[np.arange(batch_size), t] ) ) / batch_size )

ニューラルネットワークの学習では、

認識精度を「指標」にしてはいけない。

なぜなら、認識精度を指標にすると、

パラメータの微分がほとんどの場所で0

になってしまうから。

だから、損失関数が必要なのである。

手書き数字認識とバッチ処理『ゼロから作るDeep Learning』

『ゼロから作るDeep Learning』3章最後

いよいよ手書き数字認識に入る。ここでは、「学習」フェーズは完了している前提で、「推論」フェーズのみ順方向伝播方式で実施。

# MNISTという手書き数字画像セットを準備
# git clone https://github.com/oreilly-japan/deep-learning-from-scratch.git
# cd deep-learning-from-scratch/ch03
# ls ../dataset/mnist.py
# ../dataset/mnist.py
# cat mnist_check.py

import sys, os
sys.path.append(os.pardir) #親ディレクトリのファイルをインポート
from dataset.mnist import load_mnist

# load_minst((訓練画像、訓練ラベル), (テスト画像、テストラベル)
# 初回呼び出しはネットDL、2回目以降はローカルpickleファイル読込
# 引数
# normalize: 0.0..1.0に正規化
# flatten: 1次元配列化
# one_hot_label: 正解ラベルのみ1でそれ以外は0にするone-hot表現として格納するか
(x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False)

print(x_train.shape) # (60000, 784)
print(t_train.shape) # (60000,)
print(x_test.shape) # (10000, 784)
print(t_test.shape) # (10000,)

続いて、MNIST画像の表示スクリプトmnist_show.pyを参考に、保存処理mnist_save.pyを作って確認

# cat mnist_save.py
# coding: utf-8
import sys, os
sys.path.append(os.pardir)  # 親ディレクトリのファイルをインポートするための設定
import numpy as np
from dataset.mnist import load_mnist
from PIL import Image

def img_save(img):
    pil_img = Image.fromarray(np.uint8(img))
    pil_img.save('mnist_save_sample.png')

(x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False)

img = x_train[0]
label = t_train[0]
print(label)  # 5

print(img.shape)  # (784,)
img = img.reshape(28, 28)  # 形状を元の画像サイズに変形
print(img.shape)  # (28, 28)

img_save(img)

# py mnist_save.py
5
(784,)
(28, 28)

出力された画像

続いて、ニューラルネットワークの推論処理を確認

# cat neuralnet_mnist.py
# coding: utf-8
import sys, os
sys.path.append(os.pardir)  # 親ディレクトリのファイルをインポートするための設定
import numpy as np
import pickle
from dataset.mnist import load_mnist
from common.functions import sigmoid, softmax


def get_data():
  # 前処理pre-processingとして、正規化normalizationを実施
    (x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, flatten=True, one_hot_label=False)
    return x_test, t_test

# pickleファイルに保存された学習済重みパラメータの読込
def init_network():
    with open("sample_weight.pkl", 'rb') as f:
        network = pickle.load(f)
    return network


def predict(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    y = softmax(a3)

    return y


x, t = get_data()
network = init_network()
accuracy_cnt = 0
for i in range(len(x)):
    y = predict(network, x[i])
    p= np.argmax(y) # 最も確率の高い要素のインデックスを取得
    if p == t[i]:
        accuracy_cnt += 1

print("Accuracy:" + str(float(accuracy_cnt) / len(x)))
#=>Accuracy:0.9352で、
# 93.52%正しく分類できた

続いてバッチ処理

バッチbatch：ひとまとまりの入力データ束

バッチ処理によって1枚あたりの処理時間を短縮できる

# cat neuralnet_mnist_batch.py
# coding: utf-8
import sys, os
sys.path.append(os.pardir)  # 親ディレクトリのファイルをインポートするための設定
import numpy as np
import pickle
from dataset.mnist import load_mnist
from common.functions import sigmoid, softmax


def get_data():
    (x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, flatten=True, one_hot_label=False)
    return x_test, t_test


def init_network():
    with open("sample_weight.pkl", 'rb') as f:
        network = pickle.load(f)
    return network


def predict(network, x):
    w1, w2, w3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    a1 = np.dot(x, w1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, w2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, w3) + b3
    y = softmax(a3)

    return y


x, t = get_data()
network = init_network()

batch_size = 100 # バッチの数
accuracy_cnt = 0

for i in range(0, len(x), batch_size):
    x_batch = x[i:i+batch_size]
    y_batch = predict(network, x_batch)
    p = np.argmax(y_batch, axis=1)
    accuracy_cnt += np.sum(p == t[i:i+batch_size])

print("Accuracy:" + str(float(accuracy_cnt) / len(x)))

実際に比較してみると、確かに高速化していることが確認できた

# バッチなし
# time py neuralnet_mnist.py
Accuracy:0.9352

real    0m2.220s
user    0m2.859s
sys 0m0.521s

# バッチあり
# time py neuralnet_mnist_batch.py
Accuracy:0.9352

real    0m0.991s
user    0m0.857s
sys 0m0.312s

出力層の設計（分類問題で使うソフトマックス関数）『ゼロから作るDeep Learning』

『ゼロから作るDeep Learning』3章続き

# ニューラルネットワークの問題は、回帰問題と分類問題に大別できる
# 回帰問題とは、入力データから数値予測を行う問題（例　入力：人物画像　→　出力：体重予測）
# 分類問題とは、入力データがどのクラスに属するかという問題（例　入力：人物画像　→　出力：男性クラスor女性クラス）
# 回帰問題では恒等関数を使い、分類問題ではソフトマックス関数softmaxを使う
# ソフトマックス関数は、分子に入力信号の指数関数、分母にすべての入力信号の指数関数の和から構成される
def softmax(x):
  return np.exp(x) / np.sum(np.exp(x))

# 指数関数の値が巨大になりすぎる場合のオーバーフロー対策として、
# 補正値を導入する必要がある（通常、補正値は入力信号の中で最大の値）
def softmax(x):
  c = np.max(x) # オーバーフロー対策の補正値
  return np.exp(x - c) / np.sum(np.exp(x - c))

# 例
import numpy as np
import my_module as my

a = np.array([0.3, 2.9, 4.0])
y = my.softmax(a)
print(y) #=> [ 0.01821127  0.24519181  0.73659691]
print(np.sum(y)) #=> 1.0


# ソフトマックス関数の出力は、0から1の間の実数で、総和は1なので確率として解釈できる
# ソフトマックス関数を適用しても、元データの大小関係は変わらない
# 機械学習の問題を解く手順として、「学習」と「推論」の2フェーズのうち、推論フェーズではソフトマックス関数は省略する
# 出力層のニューロン数は、分類したいクラス数に設定する　（例　入力：数字画像　→　出力層：１０クラス）

ニューラルネットワーク フォワード方向処理『ゼロから作るDeep Learning』３章

『ゼロから作るDeep Learning』３章続き。

ニューラルネットワークの順方向forward処理について。

# 順方向forward処理：入力から出力方向への伝達処理。あとで逆方向backward処理について学ぶ
# 以下3層ニューラルネットワーク構成とする
# 入力層(第0層)
# 隠れ層1(第1層)
# 隠れ層2(第2層)
# 出力層(第3層)

# cat forward.py
#!/usr/bin/env python

import numpy as np
import my_module as my

def init(): #初期化
  n = {}
  # weight
  n['W1'] = np.array([ [0.1, 0.3, 0.5], [0.2, 0.4, 0.6] ])
  n['W2'] = np.array([ [0.1, 0.4], [0.2, 0.5], [0.3, 0.6] ])
  n['W3'] = np.array([ [0.1, 0.3], [0.2, 0.4] ])
  # bias
  n['b1'] = np.array([0.1, 0.2, 0.3])
  n['b2'] = np.array([0.1, 0.2])
  n['b3'] = np.array([0.1, 0.2])

  return n


def forward(n, x): #入力を出力へ変換する処理をまとめた関数
  W1, W2, W3 = n['W1'], n['W2'], n['W3']
  b1, b2, b3 = n['b1'], n['b2'], n['b3']

  # 1層目
  a1 = np.dot(x, W1) + b1
  z1 = my.sigmoid(a1)
  # 2層目
  a2 = np.dot(z1, W2) + b2
  z2 = my.sigmoid(a2)
  # 出力層
  a3 = np.dot(z2, W3) + b3
  y = my.identity(a3) #何もせずそのまま返す恒等関数

  return y


n = init()
x = np.array([1.0, 0.5])
y = forward(n, x)
print(y)

# 実行
 py forward.py
[ 0.31682708  0.69627909]

次は、出力層の設計に入る。