 『Pythonからはじめる数学入門』
『Pythonからはじめる数学入門』
3章 データを統計量で記述する
の解説です。
機械学習では、
統計がよく出てくるので、
ここでは、統計の基本をPythonで学びます。
3.1 平均を求める
まずは、平均値を求める関数です。
def calculate_mean(numbers): s = sum(numbers) #合計 N = len(numbers) #要素数 mean = s/N #平均 return mean if __name__ == '__main__': datalist = [100,60,70,900,100,200,500,500,503,600,1000,1200] mean = calculate_mean(datalist) N = len(datalist) print('要素数:{0}, 平均:{1}'.format(N, mean))
結果
要素数:12, 平均:477
3.2 中央値を求める
昇順にならべたリストの中央の要素が中央値です(リストが偶数個なら中央2要素の平均)。
中央値を求める関数です。
def calculate_median(numbers): #中央値計算 N = len(numbers) #要素数 numbers.sort() #昇順に並び替え if N % 2 == 0: m1 = int(N/2) - 1 # 整数に変換して位置合わせ m2 = int((N/2) + 1) -1 median = (numbers[m1] + numbers[m2])/2 else: m = (N+1)/2 m = int(m) - 1 median = numbers[m] return median if __name__ == '__main__': datalist = [100,60,70,900,100,200,500,500,503,600,1000,1200] median = calculate_median(datalist) N = len(datalist) print('N:{0}, 中央値:{1}'.format(N, median)) datalist.sort() print(datalist)
結果
N:12, 中央値:500 [60, 70, 100, 100, 200, 500, 500, 503, 600, 900, 1000, 1200]
3.3 最頻値を求め度数分布表を作る
最頻値は、もっとも多く出現する値です。
3.3.1 一番多い要素を見つける
要素の個数が多い順にリストを返すmost_common()を使います。
datalist = [4,2,1,2,3,4,2] from collections import Counter c = Counter(datalist) print(c.most_common()) #要素の個数が多い順に表示 print(c.most_common(2)) #上位2番目までの要素のみ表示
結果
[(2, 3), (4, 2), (1, 1), (3, 1)] [(2, 3), (4, 2)]
3.3.2 最頻値を探す
最頻値を返す関数です。
from collections import Counter def calculate_mode(numbers): c = Counter(numbers) mode = c.most_common(1) return mode[0][0] if __name__ == '__main__': scores = [7,8,6,7,5,3,3,3,5,6,1,9,1,1,2,4,0,2,3,5,2] mode = calculate_mode(scores) print('最頻値:{0}'.format(mode))
結果
最頻値:3
3.3.3 度数分布表を作る
数のリストの度数分布表の求め方です。
from collections import Counter def frequency_table(numbers): table = Counter(numbers) print('Number | Frequency') for number in table.most_common(): print('{0} | {1}'.format(number[0], number[1])) if __name__ == '__main__': scores = [7,8,6,7,5,3,3,3,5,6,1,9,1,1,2,4,0,2,3,5,2] mode = frequency_table(scores)
結果
Number | Frequency 3 | 4 1 | 3 2 | 3 5 | 3 6 | 2 7 | 2 0 | 1 4 | 1 8 | 1 9 | 1
3.4 散らばりを測る
散らばり(dispersion)とは、 データセットで数がどれだけ 平均から離れているかの統計値です。
3.4.1 数集合の範囲を決める
数集合の範囲を求める処理です。
def find_range(numbers): lowest = min(numbers) highest = max(numbers) r = highest - lowest return lowest, highest, r if __name__ == '__main__': dataset = [100,60,70,900,100,200,500,500,503,600,1000,1200] lowest, highest, r = find_range(dataset) print('Lowest:{0} Highest:{1} Range:{2}'.format(lowest, highest, r))
結果
Lowest:60 Highest:1200 Range:1140
3.4.2 分散と標準偏差を求める
分散(variance)とは、値の散らばり度合いです。
分散が大きければ、値が平均から大きく離れて、小さければ、値が平均近くにかたまっています。
def calculate_mean(numbers): s = sum(numbers) #合計 N = len(numbers) #要素数 mean = s/N #平均 return mean def find_differences(numbers): mean = calculate_mean(numbers) diff = [] for num in numbers: diff.append(num - mean) return diff def calculate_variance(numbers): #分散 diff = find_differences(numbers) squared_diff = [] for d in diff: squared_diff.append(d**2) sum_squared_diff = sum(squared_diff) variance = sum_squared_diff / len(numbers) return variance if __name__ == '__main__': datalist = [100,60,70,900,100,200,500,500,503,600,1000,1200] variance = calculate_variance(datalist) #分散 print('variance:{0}'.format(variance)) std = variance**0.5 #標準偏差 print('std:{0}'.format(std))
結果
variance:141047 std:375.562245174
3.5 2つのデータセットの相関を計算する
相関とは、2つのデータセットの関係性です。
相関係数とは、線形的な関係性を-1から1の範囲で示す統計量です。非線形関係については、別の測度が必要です。
相関係数0:線形相関がない
相関係数+1:強い正の線形相関がある
相関係数−1:強い負の線形相関がある
3.5.1 相関係数を計算する
相関係数を計算するためには、2つのデータセットの対応する要素の対を返すzip()関数を使います。
dataset1 = [1,2,3] dataset2 = [4,5,6] for x, y in zip(dataset1,dataset2): print(x,y)
結果
(1, 4) (2, 5) (3, 6)
相関係数の計算式は、以下を参照してください。
相関係数を求める処理は以下の通りです。
def find_corr_x_y(x,y): n = len(x) prod = [] for xi,yi in zip(x,y): prod.append(xi*yi) sum_prod_x_y = sum(prod) sum_x = sum(x) sum_y = sum(y) squared_sum_x = sum_x**2 squared_sum_y = sum_y**2 x_square = [] for xi in x: x_square.append(xi**2) x_square_sum = sum(x_square) y_square = [] for yi in y: y_square.append(yi**2) y_square_sum = sum(y_square) numerator = n*sum_prod_x_y - sum_x*sum_y denominator_term1 = n*x_square_sum - squared_sum_x denominator_term2 = n*y_square_sum - squared_sum_y denominator = (denominator_term1*denominator_term2)**0.5 correlation = numerator/denominator return correlation if __name__ == '__main__': data1 = [1,2,3] data2 = [1,2,3] corr = find_corr_x_y(data1,data2) print('data1 data2 correlation:{0}'.format(corr)) data3 = [1,2,3] data4 = [3,2,1] corr = find_corr_x_y(data3,data4) print('data3 data4 correlation:{0}'.format(corr)) data5 = [-93831,29999,8188] data6 = [-1,-2,1] corr = find_corr_x_y(data5,data6) print('data5 data6 correlation:{0}'.format(corr))
結果
data1 data2 correlation:1.0 data3 data4 correlation:-1.0 data5 data6 correlation:0.0243875472264
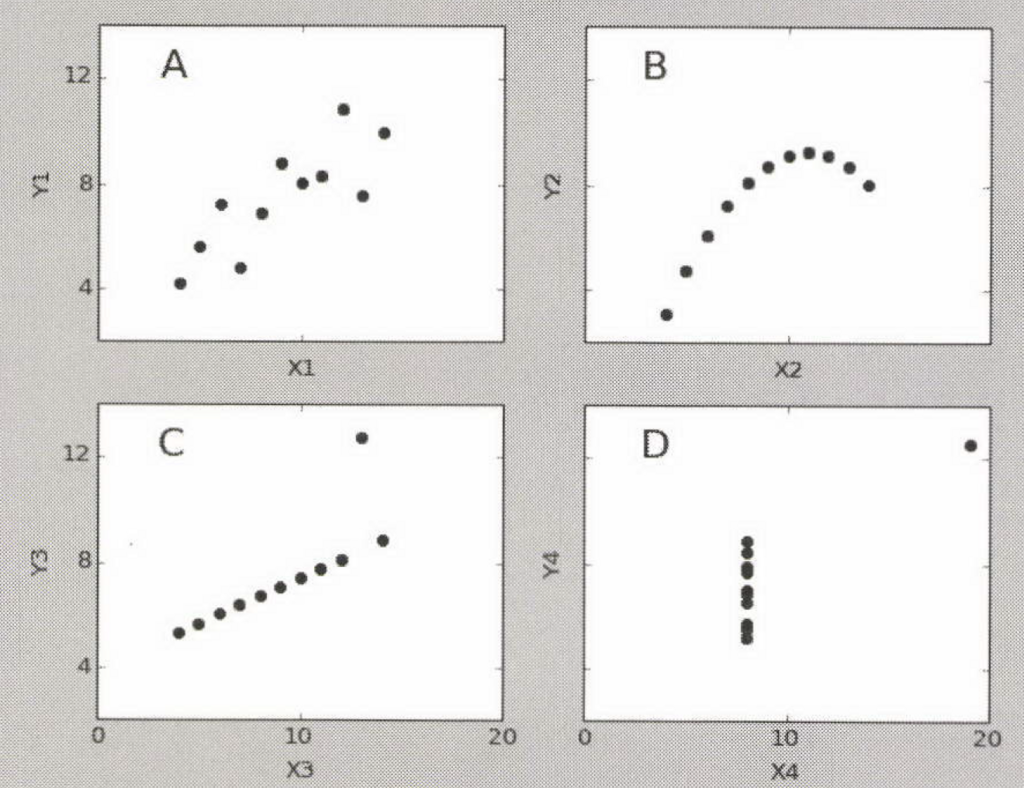
3.5.2 高校の成績と大学入試の点数
2つのデータセットのプロットを散布図で表現すれば、ビジュアルで理解できます。
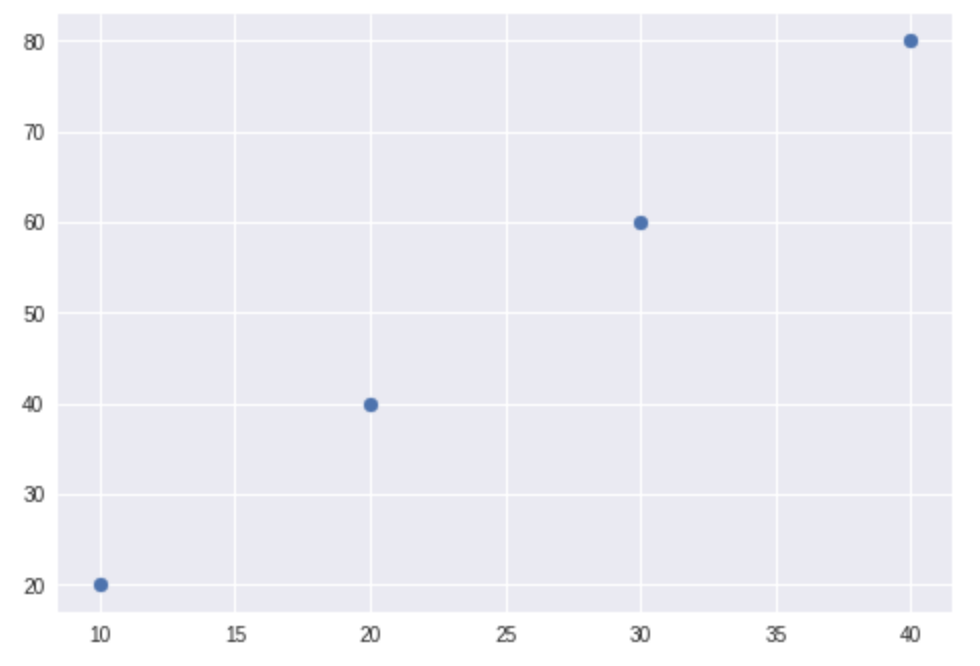
3.6 散布図
散布図は以下のように表示します。
x = [10,20,30,40] y = [20,40,60,80] import matplotlib.pyplot as plt plt.scatter(x,y) plt.show()